cash_drain_game

The Cash Drain Game §

WIP DO NOT READ YET! §

Imagine a network where every node is holding some cash. Some nodes are rich, others are in debt, and overall the books balance out to zero. The game is simple: we want to get rid of all the cash by letting nodes redistribute it to their neighbors, until everything cancels out. This is what I call the \emph{Cash Drain Game}. It’s a discrete-time process that we now make precise.

Formally, let $G=(V,P)$ be a directed graph with vertex set $V$ and transition matrix $P$, where $P(x,y)$ is the probability of moving from $x$ to $y$. Throughout, we assume $P$ is irreducible, so the network is strongly connected.

At each time $t\ge 0$, every node $x\in V$ carries some real number $C_t(x)$ that we call its \emph{cash}. The initial configuration $C_0$ is chosen so that the total cash is zero. Equivalently, we can write $C_0$ as the difference of two probability measures: [ C_0 = \mu^+ - \mu^-. ] So we are literally starting with “credits” and “debts” that balance out.

A \emph{strategy} is a sequence of subsets $\mathbf{G}=(G_t{)}_{t\ge 0}$, telling us which nodes fire at each step. When a node $x\in G_t$ fires, it trades \emph{all} of its cash—positive or negative—by distributing it among its out-neighbors according to the transition probabilities in $P$. In equations: [ C_{t+1}(x) = \begin{cases} \sum_{y \in G_t} C_t(y)P(y,x) - C_t(x), & x \in G_t, \\[6pt] \sum_{y \in G_t} C_t(y)P(y,x) + C_t(x), & x \notin G_t. \end{cases} ]

This rule can be written compactly in matrix form: [ C_{t+1} = C_t\bigl[I - I(G_t)(I-P)\bigr] ;=; C_t P(G_t), ] where $I(G_t)$ is the diagonal matrix that acts like the identity on the nodes in $G_t$ and zero elsewhere. The matrix $P(G_t)$ describes the actual redistribution of cash at time $t$: it is stochastic, but with absorbing states for nodes that do not fire.

Firing nodes is not free. Each fired node $x$ has some costs $w_x$. For example it could be its out-degree, which matches the number of cash transfers it performs. This cost is natural to think of as the “work” required, since the number of operations is proportional to the number of transactions. The cost of a firing set is thus [ \text{cost}(G_t) = \sum_{x \in G_t} w_x. ]

The objective of the Cash Drain Game is to make the system converge: positive and negative cash should meet and cancel out, so that the total $l1$ norm of the cash vector shrinks to zero. The central problem is then: given a network $G$ and an initial configuration $C_0$, can we find a strategy $\mathbf{G}$ that drives the cash to extinction, and does so at minimum total cost?

Now, is this NP-hard? how does the optimal sequence of moves looks like?

Here we consider a small example, and try different techniques to see how far can we push it. You might ask, what’s the reason to consider this problem? Is it relevant for some real world task? Indeed that is the case. But we won’ t get into it, since that spoils the fun.

The goal here is to use different techniques to solve this problem, from the basic naives one, i.e. brute force search, to elegant genetic algorithms. What can we lear from the, very heavily computed, optimal moves from tiny examples? We will try to come up with simple heuristics that can be applied to bigger instances.

Let’s consider this instance of the problem with $8$ nodes:

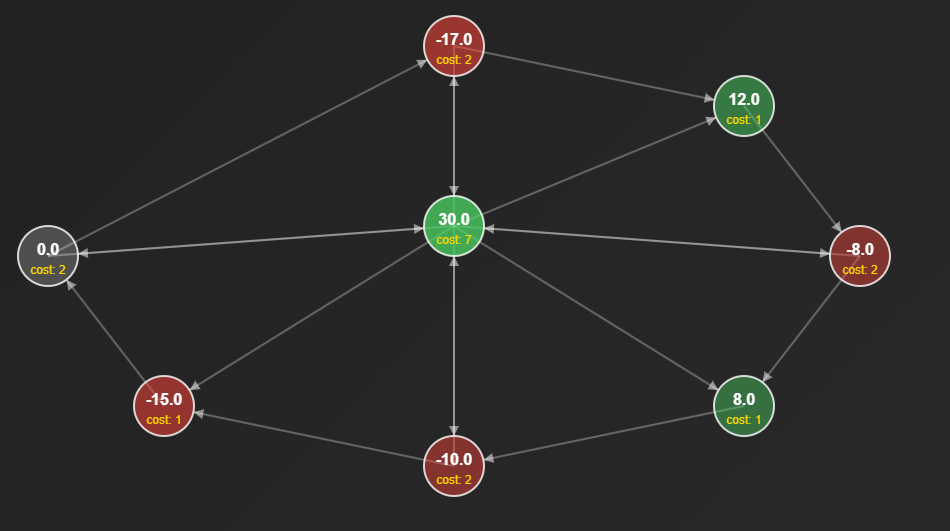
But now, some tiny examples where we can reach zero cash in finite steps (and a theorem)

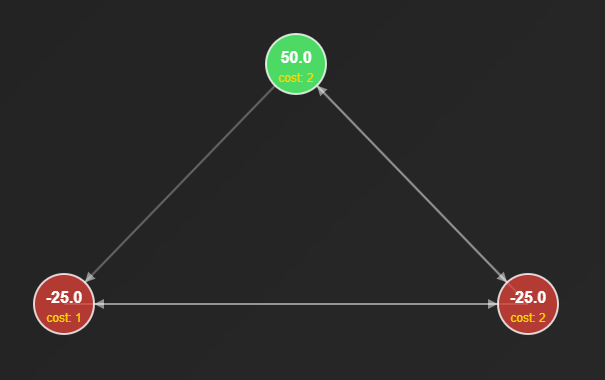
In the first case, it’s clear that the initial cash was conviniently placed. But on the second?

If we list all cycles that graph, they are not disjoint: the central node is in the intersection of all cycles! This is equivalent to say that, any sufficientyly long walk on this graph, will hit the central node: you cannot avoid it, after a while you are forced to visit it, no matter what you try to do. Then it’s easy to see that all the cash will flow into that node, in a finite amout of steps. But cash sums to zero, hence we reach a zero l1 norm! The strategy is simply never update the central node, and update all the others, until all cash reaches it! We call such nodes perfect sinks, for obvious reasons.

Actually, this is a characterization of isntances where we can finish always in finite time. Clearly, if we start with zero cash everywhere, regardless of the graph, we will finish in zero steps (which is a finite number).

Theorem The following are equivalent:

• G has at least a perfect sink
• Any cash configuration on G can reach zero cash in finite steps

For what we said, it’s easy to convince that with a perfect sink we can always find a strategy that fully drains the cash in a finite number of steps. For the converse, the crucial observation is that if we don’t have a perfect sink, then for every node $x\in V$, we can find a cycle $C$ such that $x\notin C$. But cycles acts as a “trap” for cash: say that a cycles contains only positive cash. Then no matter what happens, by updating nodes of the cycles, you cannot push away all the cash. A tiny, vanishing fraction will always reamin trapped in there. Then, if we initialzie the cash putting all positive in a cycle, and all negative in another disjoint cycle, you can never obtain a full cancellation. !FIX!

Having a perfect sink is an easy thing to check. But unfortunately, a very rare thing to observe, at least in for big graphs.

But given a initial cash distribution, can we easily say if there exists a sequence that drain the cash in finite time? In the example without perfect sink, this is indeed the case: the genetic algorithm found it! [1, 4, 7, 4, 5, 4, 6, 4, 6, 7, 4, 1, 0, 7, 7, 6, 7, 2, 1, 6, 2, 6, 2, 3, 0, 4] (remove zero cash moves).

Random Firing: Cash Drains Exponentially §

Suppose we fire nodes randomly, step after step. Intuition says the system should “average out” and cancel itself. And in fact, that’s exactly what happens: the cash decays exponentially fast to zero. This matches the rigorous results in the RLGL paper.

So, in practice, you almost always see the cash shrink rapidly.

Here I’ll add a link to a little game demo — so you can play and watch the cash drain in real time!

The catch: this only guarantees asymptotic decay. Cash gets smaller and smaller, but never quite hits zero in finite time. Which brings us to the main puzzle:

---

Finite-Step Draining: When Can We Actually Reach Zero? §

Here’s the sharp version of the question:

For a given graph $G$, does there exist a sequence of firings such that, starting from any initial configuration, the cash reaches exactly zero in finitely many steps?

This question turns out to have a clean structural answer.

---

Perfect Sinks §

First, define a perfect sink: a node that lies in the intersection of all cycles in the graph. Equivalently, every long walk eventually hits it.

If you never fire a perfect sink, all cash eventually flows into it. Since total cash is zero, positives and negatives cancel, and you’re done in finitely many steps.

Proposition 1.
If $G$ has a perfect sink, then every initial configuration drains to zero in finite time.

---

Disjoint Cycles §

On the other hand, cycles can trap cash. If the graph has two disjoint cycles, then you can place positive cash on one and negative cash on the other. They will circulate forever, never meeting to cancel.

Proposition 2.
If $G$ has two disjoint cycles, then there exists an initial configuration that does not drain in finite time.

---

The Border Case §

What if the graph has no perfect sink, but also no two disjoint cycles? Then things get tricky. Sometimes you still get finite-time draining, sometimes not.

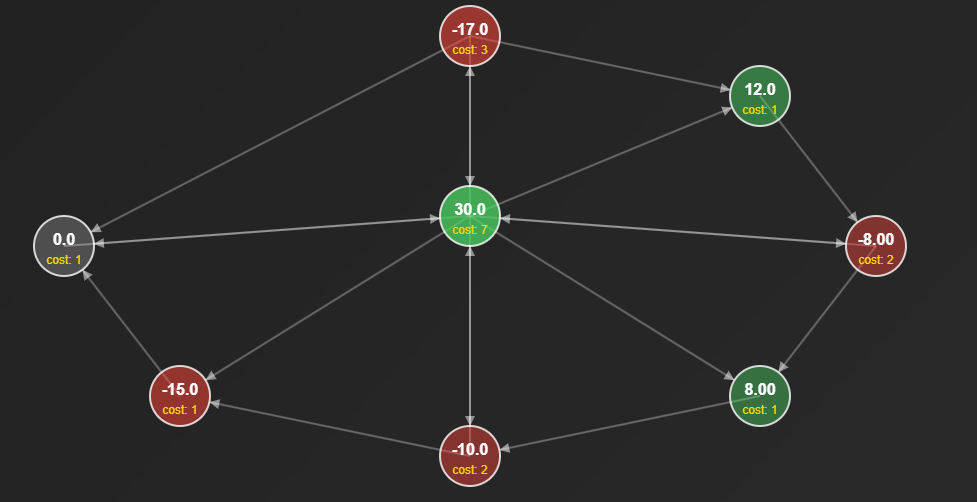
Here comes the plot twist: the very first 8-node graph I showed you (the one you might have played with!) actually lives in this border case.

And guess what? A carefully chosen sequence of firings really does drain every initial configuration to zero in finitely many steps. In fact, a genetic algorithm found the magic sequence!

Here it is (with redundant moves removed):

[1, 4, 7, 4, 5, 4, 6, 7, 4, 1, 7, 6, 7, 2, 1, 6, 2, 6, 2, 3, 4]

Magical, right? You can check that this sequence indeed drain every configuraion in finite since its associated matrix is the zero matrix.

Next, we’ll turn to experiments: brute force, heuristics, even evolutionary algorithms. They won’t solve the NP-hard optimization problem in general, but they can give us insight, and sometimes uncover “magic sequences” that algebra alone doesn’t reveal.

And yes — this game isn’t just for fun. There are real-world applications lurking underneath (who cares).