First Isomorphism theorem

Theorem Let $\varphi$ be a homomorphism from a universal algebra $A$ to $B$, let $R\subseteq Ker(\varphi )$. Then the function $\overline{\varphi }:[x]\mapsto f(x)$ (where $x$ is any memeber of the equivalence class $[x]$) is a homomorphism of $A/R$ to $B$. Furthermore, $\overline{\varphi }$ is an isomorphism iff $R=Ker(\varphi )$ and $B=\varphi (A)$ ($\varphi$ is an epi-morphism).

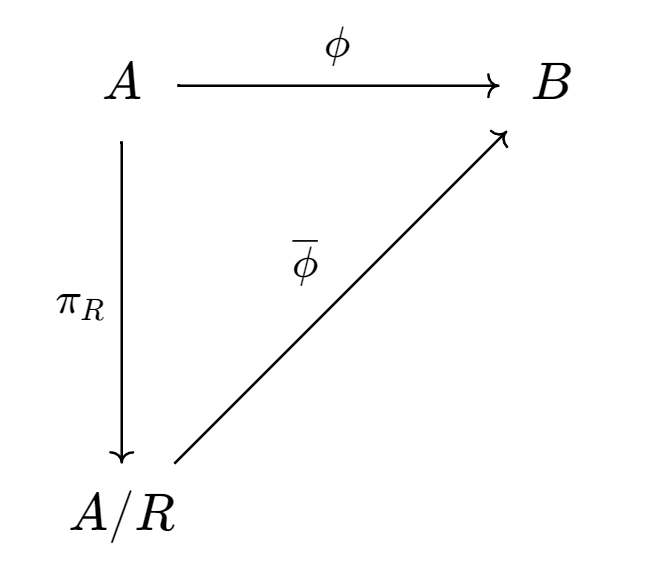
Proof First note that the mapping $\overline{\varphi }$ is well defined, if $xRy$ then $\varphi (x)=\varphi (y)$ since $R\subseteq Ker(\varphi )$. Let’s show that it’s an homorphism:

$$\overline{\varphi }([x]\cdot [y])=\overline{\varphi }([xy])=\varphi (xy)=\varphi (x)\varphi (y)=\overline{\varphi }([x])\overline{\varphi }([y])$$

It’s also clear that $\overline{\varphi }$ is sujective iff $\varphi$ is. If $R=Ker(\varphi )$, then $xRy$ iff $\varphi (x)=\varphi (y)$ (previously we only had left implies right). From this follows that $\overline{\varphi }$ is also injective, so that it’s a isomorphism:

$$\overline{\varphi }([x])=\overline{\varphi }([y])⟺\varphi (x)=\varphi (y)⟺xRy⟺[x]=[y]\square$$

Note The same proof can be extended to an arbitrary $n$-ary operation on $A$, we used binary to simplify notation.