Modello di Curie-Weiss

Modello Curie-Weiss §

E’ la versione mean-field del The Ising model, che è risolvibile analiticamente solo per $d=1$ e $d=2$ con campo esterno $h=0$. L’approssimazione di campo medio fornisce risultati qualitativamente corretti per dimensioni abbastanza elevate (esatte per $d>4$), nel caso $d=1$ sbaglia anche qualitativamente, mostrando una transizione di fase che nella soluzione esatta è assente.

L’approssimazione mean-field §

Partiamo dall’Hamiltoniana del modello di Ising in dimensione $d$, quindi un insieme di spin $\sigma =-1,1$ che vivono sul reticolo ${\mathbb{Z}}^d$. Ogni spin contribuisce all’energia totale del sistema interagendo con i suoi $2d$ primi vicini, con un termine:

$$-\sum _{j:i\sim j}J{\sigma }_i{\sigma }_j=-2d{\sigma }_i\frac{1}{2d}\sum _{j:i\sim j}{\sigma }_j$$

dove abbiamo messo in evidenza lo spin $i$, e diviso e moltiplicato per il numero di vicini. Questa riscrittura mostra come lo spin ${\sigma }_i$ interagisca con un campo medio dei sui vicini, l’ipotesi (l’approssimazione) di campo medio consiste nel sostituire a questa media sui vicini la media globale:

$$\frac{1}{2d}\sum _{j:i\sim j}{\sigma }_j\simeq \frac{1}{N}\sum _{j=1}^N{\sigma }_j=:m$$

al crescere della dimensione, questa approssimazione diventa sempre migliore, nel limite infinito dimensionale è esatta. Possiamo immaginare gli spin posizionati su un grafo completo.

Con questa approssimazione abbiamo l’Hamiltoniana del modello di Curie-Weiss:

$${\mathcal{H}}^{CW}(\sigma ):=-\frac{2dJ}{N}\sum _{i,j=1}^N{\sigma }_i{\sigma }_j-h\sum _i{\sigma }_i$$

rispetto al modello di Ising la sommatoria è su tutti le coppie $i,j$.

Misura di Gibbs §

Sia ${\Omega }_N:=\{-1,1{\}}^N$ lo spazio delle configurazioni. La misura di Gibbs su ${\Omega }_N$ è

$${\mu }^{CW}(\sigma ):=\frac{e^{-\beta \mathcal{H}(\sigma )}}{Z^{CW}}$$

Vogliamo mostrare come il modello sia paramagnetico ad alte temperaure e ferromagnetico a basse temperature.

Campo esterno $h=0$ §

Il caso di campo esterno nullo $h=0$ rende l’Hamiltoniana simmetrica per inversione $\sigma \mapsto -\sigma$. Questo implica che la densità di magnetizzazione $m_N$ abbia una distribuzione di probabilità simmetrica, ovvero:

$$⟨m{⟩}^{CW}=0$$

ci aspettiamo che ad alte temperature gli spin siano praticamente indipendenti, e sotto una certa soglia critica allineati.

Teorema §

Sia $h=0$, allora esiste una temperatura critica ${\beta }_c:=\frac{1}{2d}$ tale che:

1. Quando $\beta \le {\beta }_c$ la magnetizzazione si concentra sullo zero: $\forall ϵ>0$ $\exists N$ tale che:

$${\mu }^{CW}(m_N\in (-ϵ,ϵ))\ge 1-2e^{-cN}$$

2. Quando $\beta >{\beta }_c$, la magnetizzazione è limitata dallo zero: esiste $m^{\ast }(\beta )>0$ detta magnetizzazione spontanea, tale che per $ϵ>0$ abbastanza piccoli, esiste un $b(ϵ,\beta )>0$ tale che:

$$\mu (m\in J)\ge 1-2e^{bN}$$

dove $J$ è l’unione di due intervalli simmetrici centrati in $-m^{\ast }$ e $m^{\ast }$ di raggio $ϵ$.

• Quando $N$ è grande, per ogni temperatura maggio uguale a quella critica $m_N\simeq 0$ con alta probabilità
• Quando $N$ è grande, per ogni temperatura strettamente minore di quella critica $m_N\simeq \pm m^{\ast }(\beta )$ con probabilità vicina a $1/2$.

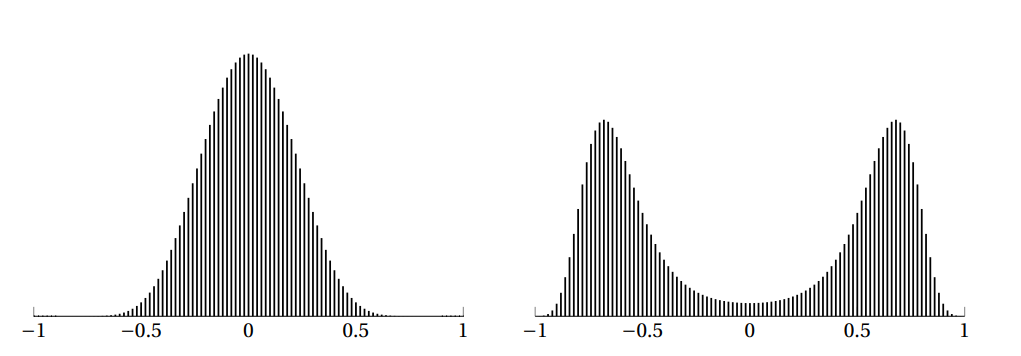
Nel limite $N\to \infty$ ho delle delta di Dirac.

In assenza di campo esterno, l’Hamiltoniana può essere riscritta in termini della magnetizzazzione media $M_N$ anzichè gli spin:

$$M_N^2={\left(\sum _{i=1}^N{\sigma }_i\right)}^2=\sum _{i,j=1}^N{\sigma }_i{\sigma }_j=N^2{m}_N^2$$ $${\mathcal{H}}^{CW}=-\frac{2dJ}{N}\sum _{i,j=1}^N{\sigma }_i{\sigma }_j=-\frac{2dJ}{N}{M}_N^2=-2dJN{m}_N^2$$

Con un abuso di notazione ridefiniamo la costa di accoppiamento:

$$J=2dJ$$

quindi abbiamo:

$${\mathcal{H}}^{CW}(m_N)=-JN{m}_N^2$$

con $m_N\in [-1,1]$ e razionale del tipo $m=\frac{2k}{N}$ con $k=-\frac{N}{2},\dots ,\frac{N}{2}$.

Abbiamo quindi un Two state system, con entropia per particella:

$$s(m)=-\frac{\left(1-m\right)}{2}\ln \left(\frac{\left(1-m\right)}{2}\right)-\frac{\left(1+m\right)}{2}\ln \left(\frac{\left(1+m\right)}{2}\right)$$

Calcoliamo la probabilità di osservare una magnetizzazione media $m$, con la misura di Gibbs:

$${\mu }^{CW}(m_N=m)=\frac{\left(\genfrac{}{}{0ex}{}{N}{N(m+1)/2}\right)e^{\beta JN{m}_N^2}}{Z^{CW}}$$

dove il coefficiente binomiale è un fattore di degenerazione, conta quante configurazione hanno una magnetizzazione media $m_N$.

Per la funzione di partizione $Z^{CW}$, siccome siamo interessati all’andamento asintotico $N\to \infty$, possiamo stimarla con il termine massimo della somma:

$$\underset{m}{\max }\left(\genfrac{}{}{0ex}{}{N}{N\frac{m+1}{2}}\right)e^{\beta JN{m}_N^2}\le Z^{CW}\le (N+1)\underset{m}{\max }\left(\genfrac{}{}{0ex}{}{N}{N\frac{m+1}{2}}\right)e^{\beta JN{m}_N^2}$$

l’esponenziale tende a far crescere $m$, mentre il coefficiente binomiale è massimo per $m=0$. Dobbiamo capire come si bilanciano i due contributi nell’ottimo. Possiamo usare la Formula di Stirling per approssimare il coefficiente binomiale, esattamente per come abbiamo fatto nel Two state system, quindi asintoticamente si comporta come $e^{Ns(m)}$.

$$Z^{CW}\le (N+1)e^{N{\max }_m\{s(m)+\beta J{m}_N^2\}}$$

osservare che $e(m)=-J{m}_N^2$, riconosco l’energia libera:

$$\beta f(m):=\beta e(m)-s(m)$$

massimizzare l’esponente equivale a minimizzare l’energia libera. Il fattore $(N+1)$ che ho nell’upperbound è ininfluente quando passo al logaritmo e al limite termodiamico:

$$\underset{N\to \infty }{\lim }\frac{-1}{\beta N}\log Z^{CW}=\underset{m}{\min }f(m)$$

Quindi la probabilità di avere una magnetizzazione media $m$ sarà:

$$\underset{N\to \infty }{\lim }-\frac{1}{\beta N}\log {\mu }^{CW}(m_N=m)=f(m)-\underset{m}{\min }f(m)$$

e la probabilità che $m\in J\subseteq [-1,1]$

\lim_{N\to\infty}-\frac{1}{\beta N}\log\mu^{CW}(m_N \in J) = \min_{m \in J} f(m)-\min_\hat m f(\hat m) = \min_{m \in J} I(m)

possiamo risolvere il problema di minimizzazione derivando (la funzione è smooth)

$$\frac{\partial I}{\partial m}=(-2\beta Jm+\frac{1}{2}\log (1-m)-\frac{1}{2}\log (1+m))=0$$ $$m=\tanh J\beta mJ=2dJ$$

studiando graficamente le soluzioni di questa equazione noto transizioni di fase sotto una certa temperatura critica, che dipenderà anche dalla dimensione $d$.

Campo esterno $h\ne 0$ §

Il campo esterno non complica le cose, infatti fattorizza nel calcolo della funzione di partizione. Cambia il punto di massimo, infatti dovrò ottimizzare:

$$\underset{m}{\max }\{N[s(m)-\beta e(m)+hm]\}$$

che in termini dell’energia libera:

$$\underset{m}{\max }\{N[-\beta f(m)+hm]\}=-\beta N\underset{m}{\min }\{f(m)-Thm\}$$

la funzione potenziale sarà:

$$\underset{N\to \infty }{\lim }\frac{-1}{\beta N}\log Z_{h\ne 0}^{CW}=\underset{m}{\min }\{f(m)-Thm\}=:\Psi (h)$$

che non è altro che la trasformata di Legendre dell’energia libera rispetto alla magnetizzazzione media, la pressione.

Studiamo il comportamento della magnetizzazzione media in funzione del campo esterno Possiamo trovare il massimo di $hm-f(m)$ derivando, essendo una funzione smooth (analitica), ottenendo una nuova equazione di autoconsistenza

$$m=\tanh [\beta Jm+h]$$

che come prima ammette sempre almeno una soluzione. Nel caso $\beta >{\beta }_c$ i imiti destro e sinistro della magnetizzazzione $m(h)$ non coincidono, siamo nella fase ferromagnetica. Se invece $\beta \le {\beta }_c$ entrambi i limiti fanno zero, siamo nella fase paramagnetica.

Studiamo ora la pressione, scrivendola con la magnetizzazzione in cui si ottiene il massimo, diventa

$$\Psi (h)=h{m}^{\ast }-f(m^{\ast })$$

dove con $m^{\ast }$ abbiamo indicato la magnetizzazzione che massimizza l’argomento della trasformata di legender (dipenderà sia dal campo esterno che dalla temperatura). Derivando

$$\frac{\partial \Psi (h)}{\partial h}=m^{\ast }$$

i ragionamento di prima sulla magnetizzazzione media $m^{\ast }$ si ripetono qui con i limiti destro e sinistro della deriata della pressione, che diventa dunque non derivabile in $h=0$ quando $\beta >{\beta }_c$.

Caratterizzazzione della transizione di fase §

Studiando le soluzioni $m^{\ast }$ dell’equazione di autoconsistenza otteniamo i punti stazionari dell’energia libera. Gli stati di equilibrio saranno i minimi.

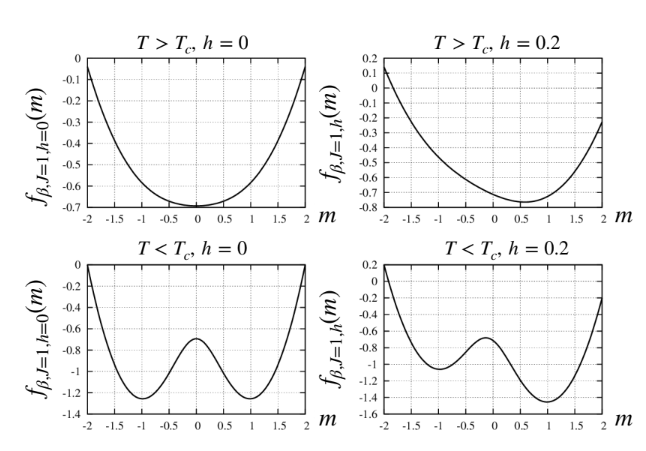
Osserviamo come l’energia libera sia simmetrica in assenza di campo esterno $h$. Sotto la temperatura critica appaiono due minimi (simmetrici), al di sopra l’unico minimo è quello di magnetizzazzione nulla.

La soglia critica ${\beta }_c$ si ottengono quando la derivata della tangente iperbolica diventa maggiore di uno:

$$\beta 2dJ\ge 1⟹{\beta }_c=\frac{1}{2dJ}$$

dipende quindi dalla dimensione del sistema $d$.

usando l’identità $|\tanh z|\le |z|$ si vede facilmente che

$$|m|\le \beta J|m|$$

quindi nel caso $\beta J<1$ l’unica soluzione possibile è $m=0$, ovvero fase paramagnetica.