Problema di Riemann

Problema di cauchy di una legge di conservazione con condizione iniziale costante a tratti con una discontinuità. 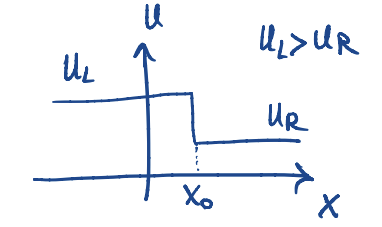Interessante perchè compaiono fenomini come onde di shock e rarefazione.

Studiamo come si comporta linear advection con questa condizione iniziale. Ci aspettiamo come al solito che la soluzione sia la condizione iniziale che viaggia con velocità costante, spostando la discontinuità. Ma la condizione iniziale non è derivabile in un punto! Non soddisfa la forma differenziale della legge di conservazine, ma quella integrale:

$$\frac{d}{dt}{\int }_0^L\rho (t,x)dx+a[\rho (t,L)-\rho (t,0)]=0$$

testiamo la soluzione ${\rho }_0(x-at)$ . Assumiamo che la discontinuità si trovi in $0<x_0<L$ al tempo zero. Supponiamo inoltre che $at<L$.

$$\frac{d}{dt}((x_0+ta){\rho }_L+(L-x_0-at){\rho }_R)+a[{\rho }_0(L-at)-{\rho }_0(-at)]$$ $$a[{\rho }_L-{\rho }_R]+a[{\rho }_R-{\rho }_L]=0$$

$QED$

Modello LWR §

Studiamo il modello macroscopico del traffico LWR con la chiusura di Green-Shield. Il problema di Riemann associato può essere cisto come la partenza dopo un semaforo rosso: a sinistra densità costante massima, a destra nulla.

Rarefazione §

Approssiamo la condizione iniziale con una funzione per cui possiamo calcolare le caratteristiche (questo approccio fallisce con la condizione di riemann perchè abbiamo una regione vuota, non raggiunta da una caratteristica), in maniera tale che ${\lim }_{ϵ\to 0}{g}_{ϵ}={\rho }_0$ . scegliamo:

$$g_{ϵ}(x)=\{\begin{array}{l}{\rho }_{M}x\ge 0\\ {\rho }_M(1-\frac{x}{ϵ})0<x<ϵ\\ 0x\ge ϵ\end{array}$$

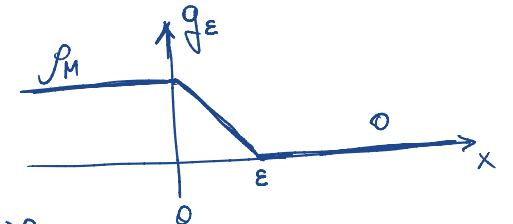
Ricordiamo che la velocità con la chiusura di GS è:

$$q^{\prime }(\rho )=v_m(1-\frac{2\rho }{{\rho }_M})$$

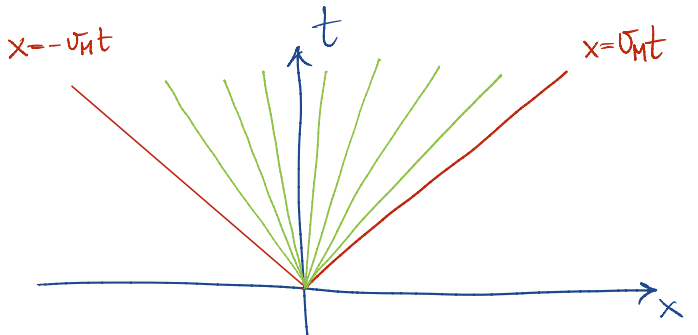
Si vede che con la condizione discontinua si hanno due velocità costanti per le caratteristiche: $-v_m$ e $v_m$ per le due regioni, creando una zona non raggiunta: Con la nuova condizione iniziale invece abbiamo nella zona vuota un ventaglio di caratteristiche detto rarefaction fan

Shock §

Il caso in cui la condizione iniziale è maggiore a destra (formazione di una cosa di traffico), osserviamo come la discontinuità invece si smussarsi in un’onda di rarefazione, si propaga all’indietro: abbiamo uno shock, che rispetta la condizione di Rankine-Hugoniot.

Infatti con questa condizione iniziale le caratteristiche si intersecano, e la soluzione va intesa in senso debole.