Let be a Markov chain with transition matrix . The first hitting time of a subset of states is the random variable defined by
with the usual convenction that the infimum of the empty set is . Remark Note that it’s a stopping time.
The probability starting from state that ever hits is
when is a closed class, is called an absorption probability.
The mean hitting time for reaching is given by
Computing and
Consider the example
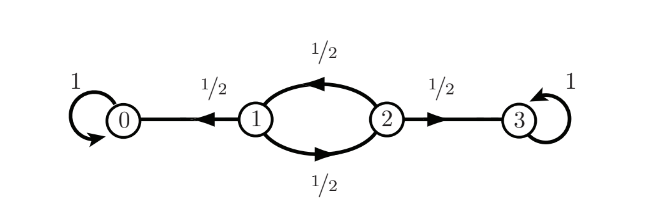
it’s a state Markov chain with absorbing states and . Let and . Clearly,
and
- these linear systems can be solved to obtain , and .
Theorem The vector of hitting probabilities is the minimal non-negative solution to the system of linear equations
In matrix form where is the matrix obtained by removing
the -th row and column when .
Proof We first show that satisfies this equations. If then , so (is finite a.s.). If
since the events form a partition of . Using the definition of conditional probability
note that . Given that , . Then
We can define a “new” Markov chain that w.r.t is by the Markov property.
so that
Suppose now that is any solution, then for . Suppose , then
substitute for to obtain
we can reiterate the substitution, after steps one gets
since is non-negative, so is the last term. Notice that the remaining terms add to the probability of (each term is the probability of . Then
we can take the limit as on both sides, and by Continuity of mesure we get the desired inequality.
Theorem The vector of mean hitting time is the minimal non-negative solution to the system of linear equations
Proof First we show that solves these equations. i \in Ak_i^A = 0i \notin A$ then, using first step analysis:
we can exchange the sums by Fubini’s theorem (all the terms are non-negative), and since , and using the weak Markov property
we now change the index to
We need to prove that if is another non negative solution, then . The strategy is the same as in the previous proof (repeated substitution). Note that since if , we can omit these terms in the sum over all states. Let , then
where , since is non-negative. Repeating the substitution times one gets:
taking the limit on both sides one gets the definition of on the right.