Ensemble microcanonico

Enseble Microcanonico §

Segue subito in maniera maturale dall’ipotesi ergodica (Boltzmann lo chiamava “Ergode”) e di stato di equilibrio come distribuzione stazionaria:

$$\mu (\Delta )=\{\begin{array}{l}\frac{1}{N(U,V)}\text{ se }U(\Delta )\in [E-DE,E]\\ 0\text{ altrimenti }\end{array}$$

con

$$N(U,V)=\sum _{U-DE\le U(\Delta )\le E}1$$

ovvero il numero di cellette con energia e volume compatibile.

La quantità $DE$ è un’incertezza macroscopica sul vincolo dell’energia.

Boltzmann dimostrò l’ortodicità del microcanonico trovando l’entropia:

$$T=\frac{2}{3k_B}\frac{T(\mu )}{N},S(\mu )=k_B\log N(U,V)$$

Si può verificare direttamente, definendo le versioni intensive, che nel limite termodinamico rispettano la condizione di ortodicità.

Verifica ortodicità §

La verifica è molto più complicata di quella del Canonico, e risulta valida solo nel limite termodinamico.

Differenziamo l’entropia definita sopra:

$$dS=k_B\left(\frac{1}{N(U,V)}\frac{\partial N}{\partial U}dU+\frac{1}{N(U,V)}\frac{\partial N}{\partial V}dV\right)$$

Il problema è valutare le derivate della funzione di partizione microcanonica.

Esistenza della funzione entropia §

Il limite termodinamico per il microcanonico assume la forma:

$$\underset{N\to \infty }{\lim }\frac{1}{N}S(U,V,N)=s(e,v)$$

con $U=eN$ e $V=vN$.

Ha senso parlare di questo limite? Ipotesi affinchè esista?

Esplicitando il limite precedente ma mandando il volume all’infinito:

$$s(u,v)=\underset{V\to \infty }{\lim }\frac{k_B}{N}\log {\int }_{\mathcal{H}\le U}\frac{dpdq}{N!h^{3N}}$$

con $\frac{N}{V}=\rho$ e $\frac{U}{V}=u$.

Mandare il numero di particelle all’infinito è straightforward, ma mandare ad infinito un volume? Ecco una difficoltà.

La parte cinetica è semplice da trattare, la complessità sta nel potenziale. Le condizioni che servono a garantire l’esistenza, sono due:

1. Temperatezza Sia $\Phi (x)$ un interazione di coppia (pair potential). L’energia potenziale di un sistema di $N$ particelle si scrive:

$$U(q_1,\dots ,q_N)=\sum _{1\le i\le j}^N\Phi (|q_i-q_j|)$$ $$\Phi (x)\le A|x{|}^{-\lambda }\forall |x|\ge R_0$$

con $A\ge 0$, $\lambda >d$ dove $d$ è la dimensione del sistema (es. 3). Diamo un’intuizione sul significato della temperatezza: Calcoliamo l’energia d’interazione tra una particella posta nell’origine con altre disposte con una certa densità costante tutt’attorno, in un volume infinito:

$$U=\rho {\int }_{|x|>R_0}\Phi (x)dx\le A\rho {\int }_{|x|>R_0}|x{|}^{-\lambda }dx=K{\int }_{R_0}^{\infty }{t}^{d-\lambda -1}dt=K{\left[\frac{t^{d-\lambda }}{d-\lambda }\right]}_{R_0}^{\infty }$$

l’integrale converge con l’ipotesi di temperatezza: Ci sta dicendo che la parte positiva dell’energia d’interazione a grande distanze diventa trascurabile.

Lavoreremo con il semplice caso di interazioni abbiano un range finito $r_0$, che equivale a porre $A=0$.

2. Diamo anche una condizione sulla parte negativa del potenziale, con una condizione di stabilità:

$$U(q_1,\dots ,q_N)\ge -BN$$

per una costante positiva $B$. Questa richiesta evita che le particelle “collassino”, è un bound inferiore sul potenziale. Ci servirà per calcolare un upper bound sull’entropia, limita gli stati accessibili.

Consideriamo l’ensemble canonico con un potenziale con un lower bound del tipo $-B{N}^k$, calcoliamo la funzione di partizione configurazionale:

$$Z_q(\beta ,V,N)=\int e^{-\beta U(q)}\frac{dq}{h^{3N}N!}\le \int e^{\beta B{N}^k}\frac{dq}{h^{3N}N!}={\left(\frac{e^{\beta B(N^{k-1})}eV}{h^{3}N}\right)}^N$$

L’energia libera di Helmotz è proporzionale al logaritmo:

$$F\sim N^k\beta B+N\log \frac{v}{h^3}$$

vediamo che nel limite termodinamico, l’energia libera per particella diverge a meno che $k=1$, ovvero se il potenziale non è stabile.

1. Convessità del ground state rispetto alla densità Consideriamo una sequenza di scatole, e di $N$ e $U$. Le scatole $B_n^{\prime }$ hanno dimensione $L_n^{\prime }=2^n{L}_0-r_0$, e sono contenute al centro di scatole più grandi $B_n$ di dimensione $2^n{L}_0$.

Il volume di queste scatole è $|B_n|=2^{3n}{L}_0^3$.

Ora un dettaglio “tecnico”, vogliamo definire il numero di particelle data la densità, tramite il volume delle scatole, ma queste hanno valori precisi: per ottenere un numero intero di particelle dobbiamo prima lavorare con densità diadiche:

$$\rho =m{2}^{-3s}{L}_0^{-3}$$

con $m,s$ interi positivi. Infatti:

$$N_n=\rho |B_n|=m{2}^{-3s}{L}_0^{-3}{2}^{3n}{L}_0^3=m{2}^{3(n-s)}$$

quindi se $n\ge s$ ho proprio quello che volevo.

Possiamo definire la densità di energia del ground state $e_{\rho }$ alla densità $\rho$ come:

$$e_{\rho }=\stackrel{\ast }{\inf }\frac{\Phi (q_1,\dots ,q_{N_n})}{|B_n|}\ge -B\rho$$

l’estremo inferiore del potenziale (l’energia cinetica è nulla al ground state) è valutato con il vincolo aggiuntivo che $q_i\in B_n^{\prime }$, quindi nelle scatole interne su tutte le configurazione e per ogni $n\ge s$. La disuguaglianza è la definizione di stabilità del potenziale.

Aggiungiamo un vincolo: dentro $B_n^{\prime }$ sono contenute $8$ $B_{n-1}^{\prime }$, quindi fisso il numero di particelle in $4$ di queste a ${\rho }_1|B_{n-1}|$ e ${\rho }_2|B_{n-1}|$ per le altre quattro, con $\rho =\frac{{\rho }_1+{\rho }_2}{2}$ ottengo lo stesso numero di particelle di prima, ma avendo aggiunto un vincolo. Inoltre essendo le scatole separate da $r_0$ l’energia configurazionale delle scatole è semplicemente la somma.

$$e_{\rho }\le \frac{1}{2}(e_{{\rho }_1}+e_{{\rho }_2})$$

Abbiamo la quasi-convessità: è convessa sulle densità diadiche, che sono dense nei reali. Per estenderla ci serve la continuità, siccome $e_{\rho }\to 0$ quando $\rho \to 0$, infatti può essere maggiorata dall’energia del ground state per una qualunque disposizione, es. quella omogenea:

$$e_{\rho }\le \frac{N(N-1)}{2|B_n|}\varphi ({\rho }^{-\frac{1}{3}})=\rho \frac{(N-1)}{2}\varphi ({\rho }^{-\frac{1}{3}})$$

definendo $e_0=0$ (zero non è diadico) otteniamo che $\rho \mapsto e_{\rho }$ è continua sui diadici e su zero. Ma allora possiamo estenderla per densità reali.

2. Upper bound uniforme sull’entropia

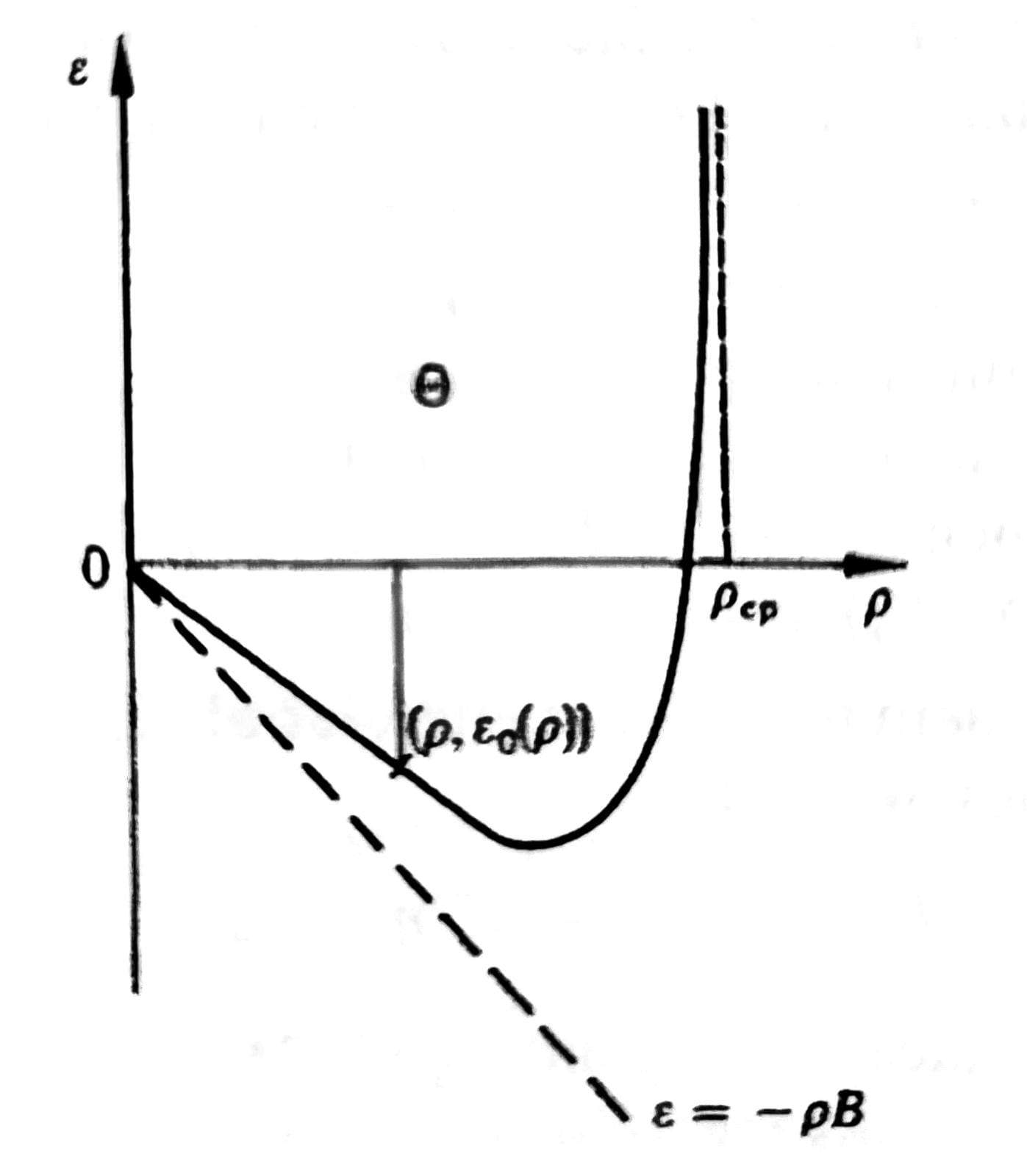
Chiamiamo $\Theta$ l’epigrafo della funzione $e_{\rho }$. Sia $(\rho ,e)\in \Theta$ un punto interno con $\rho$ diadica e $e>e_{\rho }$. Dato $\rho ,e,V^{\prime }\subset V$. Per densità $\rho$ multiple intere di $2^{-3n}{L}_0^{-3}$, definiamo una corrispondente entropia microcanonica:

$${\sigma }_n(\rho ,e)=\frac{1}{|B_n|}\log \Sigma (\rho ,e,B_n^{\prime })$$

Osservazione è leggermente diversa dalla definzione solita: sto dividendo per un volume leggermente più grande!

Possiamo effetturare il bound:

$${\sigma }_n(\rho ,e)\le \frac{1}{|B_n|}\log \frac{\Omega (3N_n)(\sqrt{2m|B_n|(e-e_{\rho })}{)}^{3N_n}}{h^{3N_n}{N}_n^{N_n}{e}^{-N_n}\sqrt{2\pi N_n}}|B_n^{\prime }{|}^{N_n}\le \rho \log \frac{(4m{e}^{5/3}/3{)}^{3/2}(e-e_{\rho }{)}^{3/2}}{h^3{\rho }^{5/2}}$$

abbiamo sfruttato il fatto che $e\rho$ è l’inf dell’energia configurazionale a densità $\rho$. $\Omega (m)=\frac{{\sqrt{2\pi }}^{m/2}}{\Gamma (\frac{m}{2})}$ è la superficie delle sfera unitaria in $m$ dimensioni (si veda Volume della palla n dimensionale). L’energia di ground state dipende ancora da $n$, ma utilizzando la condizione di stabilità otteniamo un bound uniforme in n.

Quindi la linearità in $N$ sulla condizione di stabilità è fondamentale, permette di far comparire la densità quando si divide per il volume:

$$e_{\rho }\ge -B\frac{N_n}{|B_n|}=-B\rho$$

3. Quasi concavità dell’entropia a volume finito

La funzione ${\sigma }_n(\rho ,e)$ ha la proprietà di essere midpoint-convessa. Infatti supponiamo di prendere:

$$\rho =\frac{1}{2}({\rho }_1+{\rho }_2)e=\frac{1}{2}(e_1+e_2)$$

con densità diadiche e energie maggiori del ground state. Ora viene un argomento combinatorio. Sia $\Sigma (\rho ,e,B_{n+1}^{\prime })$ la funzione di partizioni, i.e. il numero di stati del sistema fissata la densità, l’energia ed il volume. Dentro $B_{n+1}^{\prime }$ sono contenute $8$ copie di $B_n^{\prime }$, separate da un corridoio $r_0$ e quindi non interagenti. Aggiugiamo un vincolo, imponendo di mettere in $4$ delle scatole esattamente $N_1={\rho }_1|B_n|$ e $N_2={\rho }_2|B_n|$ nelle restanti $4$. In tale modo $N=4(N_1+N_2)$. Il numero di modi in cui posso fare questa cosa, ovvero scegliere come assegnare le particelle a ciascuno degli $8$ cubi è:

$$\frac{N!}{N_1{!}^4{N}_2{!}^4}$$

quindi vale:

$$\Sigma (\rho ,e,B_{n+1}^{\prime })\ge \Sigma ({\rho }_1,e_1,B_n^{\prime }{)}^4\Sigma ({\rho }_2,e_2,B_n^{\prime }{)}^4$$

In termini di ${\sigma }_n$:

$${\sigma }_{n+1}(\rho ,e)\ge \frac{1}{2}({\sigma }_n({\rho }_1,e_1)+{\sigma }_n({\rho }_2,e_2))$$

Nota: per estendere ${\sigma }_n$ a densità non diadiche, ricorriamo all’interpolazione linare:

$${\sigma }_n({\rho }^{\ast },e)=t{\sigma }_n({\rho }_1,e)+(1-t){\sigma }_n({\rho }_2,e){\rho }^{\ast }=t{\rho }_1+(1-t){\rho }_{2}t\in [0,1]$$

Questa definizione preserva i risultati che abbiamo ottenuto, ovvero l’upper bound sull’entropia e la non-descrescenza in $n$ (perchè è una combinazione convessa!).

Nota: i diadici sono densi, ma solo se $n\to \infty$. Nel nostro caso $n$ è finito, quindi sono ben definiti i diadici ${\rho }_1$ e ${\rho }_2$ attorno a $\rho$.

4. Monotonia dell’entropia come funzione di n

Si vede molto semplicemente che:

$${\sigma }_{n+1}(\rho ,e)=\frac{1}{|B_{n+1}|}\log \Sigma (\rho ,e,B_{n+1}^{\prime })\ge \frac{1}{|B_{n+1}|}\log \Sigma (\rho ,e,B_n^{\prime }{)}^8={\sigma }_n(\rho ,e)$$

La monotonia implica che il limite $n\to \infty$ di ${\sigma }_n(\rho ,e)$ esista per ogni $\rho$ diadica e $e>e_{\rho }$. Ma la sequenza converge anche per $\rho$ non diadiche per la quasi convessità, uniformemente per ogni insieme chiuso nell’interno della regione convessa $A$. Questo segue dalla proprietà del limite di sequenze di funzioni convesse monotone.

L’upper bound uniforme e la quasi convessità implicano che al funzione limite $s(\rho ,e)$ sarà concava e limitata nella regione interna di $A$, quindi continua.

4. Indipendenza dalla particolare sequenza di densità e volumi

Abbiamo dimostrato l’esistenza del limite per una sequenza speciale di cubi, liberiamoci di qualche ipotesi restrittiva. Per ora consideriamo sequenza generiche di cubi con lato $L\to \infty$. L’idea è scomporli e ricondurci al caso precedente, l’errore commesso tende a zero.

Sia ${\rho }_0=\rho +ϵ$ con ${\rho }_0$ diadica, e $e_0=e-\eta$ con $ϵ,\eta$ “piccoli”.

Scomponiamo il generico cubo $B$ in scatole $B_n$ di dimensione $L_n=2^n{L}_0$. Il numero di scatole necessario sarà il cubo della parte intera $\left[\frac{L}{L_n}\right]$. La differenza del volume dell’unione dei cubi $B_n$ sarà al massimo $|B|-|\cup B_n|\le (8L^2{L}_n)$. Le scatole interne $B_n^{\prime }$ invece un po’ meno:

$$|\cup B_n^{\prime }|=|\cup B_n|-6(r_0{L}_n^2){\left[\frac{L}{L_n}\right]}^3\ge |B|-(3L^2{L}_n)-6(\frac{r_0}{2}{L}_n^2){\left[\frac{L}{L_n}\right]}^3$$ $$=|B|\left(1-3\frac{L_n}{L}-3\frac{r_0}{L_n}\right)$$

Dove abbiamo usato il fatto che $[x]\le x$. Se $N,L$ sono abbastanza grandi in maniera tale che

$$\left(1-3\frac{L_n}{L}-3\frac{r_0}{L_n}\right){\rho }_0>{\rho }_0-\frac{ϵ}{2}>\rho$$

notiamo che mettendo in ogni scatola $B_n^{\prime }$ un numero di particelle $N_n={\rho }_0|B_n|$ finiamo per mettere nel volume totale $B$ più di $N$ particelle ($N=\rho |B|$).

Per ottenere quindi un numero esatto di particelle, riempiamo con $N_n={\rho }_0|B_n^{\prime }|$ solo un numero di scatole pari a $\left[\frac{N}{N_n}\right]$, e mettiamo in una delle rimanenti la differenza $n<N_n$ per arrivare al numero esatto $N$.

Quindi avremo $\left[\frac{N}{N_n}\right]$ scatole con energia $\le e_0|B_n|$. In conclusione:

$$\frac{1}{|B|}\log \Sigma (\rho ,e,B)\ge \frac{1}{|B|}(\log \Sigma ({\rho }_0,e_0,B_n^{\prime }{)}^{\left[\frac{N}{N_n}\right]}+C_n)$$

dove $C_n$ è un bound su $\log \Sigma ({\rho }^{\prime },e^{\prime })$ per l’ultima scatola, con ${\rho }^{\prime }=\frac{n}{|B_n|}$ ed $e^{\prime }$ un valore arbitrario ma sufficientemente grande (maggiore del ground state).

Questo significa (tenendo conto dell’arbitrarietà di $n$) che:

$$\underset{L\to \infty }{\mathrm{liminf}}\frac{1}{|B|}\log \Sigma (\rho ,e,B)\ge {\sigma }_n({\rho }_0,e_0)\to \sigma ({\rho }_0,e_0)$$

perchè $\frac{1}{|B|}{C}_n\to 0$ e $\frac{1}{|B|}\left[\frac{N}{N_n}\right]\to \frac{\rho }{{\rho }_n}\frac{1}{|B_n|}$.

5. Volumi generici nel senso di Fisher

Ora dimostriamo che il limite vale per ogni sequenza di volumi che tende all’infinito nel senso di Fisher:

$$\frac{|B_{+}(l)|-|B_{-}(l)|}{|B|}\le A{\left(\frac{l}{diam(B)}\right)}^{\alpha }$$

con $A,\alpha >0$. Abbiamo scomposto il volime in cubi interni ed esterni di lato $l$. Questa richiesta ci assicura che il bordo non cresca troppo velocemente rispetto al volume.