Risolvere sistemi lineari §

Consideriamo il problema

$$Ax=b$$

con $A\in {\mathbb{C}}^{m\times n}$ , $b\in {\mathbb{C}}^m$ e $x\in {\mathbb{C}}^n$. Il problema è ben posto se esiste unica la soluzione, ovvero se $A$ è invertibile. A livello teorico, per calcolare la soluzione possiamo usare la formula di Cramer:

$$x_i=\frac{{\Delta }_i}{\det (A)}$$

con ${\Delta }_i$ il determinante della matrice dove alla colonna $i$ è stata sostituito il vettore noto $b$. Tuttavia questa formula è assai inefficiente: calcolare il determinante ricorsivamente costa è dell’ordine $n!$.

Per questo motivo sono stati sviluppati metodi numerici alternativi alla regola di Cramer, che vengono detti diretti se conducono alla soluzione del sistema dopo un numero finito di passi o iterativi se ne richiedono (teoricamente) un numero infinito.

Sistemi triangolari §

Data la loro semplice struttura richiedono $n^2$ flops per essere risolti.

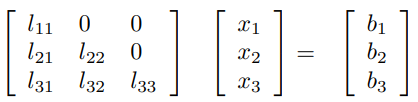
La matrice $L$ è non singolare se e solo se gli elementi diagonali $l_{ii}\ne 0$ (sono i pivot). In questo caso possiamo sequenzialmente trovare il vettore soluzione:

$$\begin{array}{rl}& x_1=\frac{b_1}{l_{11}}\\ & x_2=\frac{b_2-l_{21}{x}_1}{l_{22}}\\ & x_3=\frac{b_3-l_{31}{x}_1-l_{32}{x}_2}{l_{33}}\end{array}$$

In generale, sia $L$ triangolare inferiore e non singolare, il problema:

$$Lx=b$$

può essere risolto come prima, forward substitution:

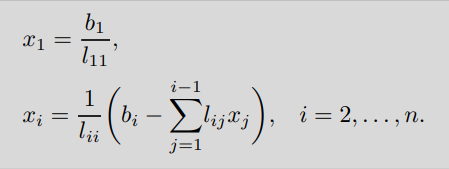
Analgomanete per sistemi triangolari inferiori:

$$Ux=b$$

con la backward substitution, che invece inizia calcoalndo $x_n$.

Costo computazionale §

Questi algoritmi effettuano $n\frac{(n+1)}{2}$ divisioni/moltiplicazioni e $n\frac{(n-1)}{2}$ addizioni/sottrazioni, quindi in totale $n^2$ FLOPS.