Lattice gas

Lattice Gas §

Ipotesi: ogni sito può essere occupato o meno da una sola particella, quindi c’è l’ipotesi di hard core. Inoltre la forza è attrattiva, ed a coppia:

Chiamiamo ${\Phi }_2(i,j)$ con $K(i,j)$.

1. essendo attrattiva è negativa, la definiamo positiva: $-K(i,j)\le 0$
2. a lungo raggio la forza decresce: $K(i,k)\to 0$ quando $\Vert i-j{\Vert }_{\infty }\to 0$.
3. invariante per traslazioni

$$K(i,j)=K(i+a,j+a)\forall a\in {\mathbb{Z}}^d$$

questo implica, traslando per l’opposto di uno dei due siti:

$$K(i,j)=K(0,j-i)⟹K(i-j)$$

ovvero che è funzione della differenza.

L’energia d’interazione totale è quindi:

$$U=-\sum _{(i,j)\subset \Lambda }K(i,j)$$

Costruiamo un tipico potenziale d’interazione.

Indichiamo il numero di occupazione della cella $i$ con ${\eta }_i$. Per l’ipotesi di prima, nel nostro modello sarà ${\eta }_i=0,1$. E’ lo stato del sistema.

L’energia del sistema sarà quella dovuta alle interazioni dei siti occupati:

$$\mathcal{H}(\eta ):=-\sum _{(i,j)\subset \Lambda }K(i,j){\eta }_i{\eta }_j$$

Aggiungiamo una richiesta sul potenziale d’interazione: che sia sommabile che è equivalente a dire che l’interazione con una particella ed il resto del sistema è limitata:

$$\underset{i\in {\mathbb{Z}}^d}{\sup }\left\{\sum _{j\ne i}K(i,j)\right\}=\sum _{i\ne 0}K(0,i)=\kappa <\infty$$

come conseguenza dell’invarianza per traslazioni. Il numero totale di particelle nella regione sarà:

$$N(\Lambda ):=\sum _{i\in \Lambda }{\eta }_i$$

e la densità empirica

$${\rho }_{\Lambda }:=\frac{N(\Lambda )}{|\Lambda |}$$

Data l’Hamiltoniana, possiamo definire le distribuzioni Canonica e Gran canonica.

Il potenziale associato è l’energia libera

$$f_{\beta ,\Lambda ,N}:=-\frac{1}{\beta |\Lambda |}\log Z_{\beta ,\Lambda ,N}$$

Esistenza dell’energia libera §

Definiamo una sequenza di volumi finiti che converge a ${\mathbb{Z}}^d$. Diciamo che ${\Lambda }_n\uparrow {\mathbb{Z}}^d$ se:

1. ${\Lambda }_n\subset {\Lambda }_{n+1}$
2. $\bigcup {\Lambda }_n={\mathbb{Z}}^d$

Torna utile, per trascurare le condizioni di bordo, richiedere una cosa aggiuntiva:

$$\underset{n\to \infty }{\lim }\frac{|{\partial }^{in}{\Lambda }_n|}{|{\Lambda }_n|}=0{\partial }^{in}\Lambda :=\{i\in \Lambda |\exists j\notin \Lambda \wedge i\sim j\}$$

dove il bordo è alla solita maniera. Diciamo che ${\Lambda }_n\Uparrow {\mathbb{Z}}^d$ nel senso di Van Hove.

Una sequenza semplice che soddisfa tutti questi requisiti è quella dei cubi:

$$B(n)=\{-n,\dots ,n{\}}^d$$

Teorema §

Sia ${\Lambda }_n\Uparrow {\mathbb{Z}}^d$ una sequenza nel senso di Van Hove. Sia $\rho \in [0,1]$ ed $N_n\in \mathbb{N}$ tale che $\frac{N_n}{|{\Lambda }_n|}\to \rho$. Il limite

$$\underset{n\to \infty }{\lim }{f}_{{\Lambda }_n;\beta }(\rho )=f_{\beta }(\rho )$$

esiste, non dipende dalla scelta delle sequenza ${\Lambda }_n$ e $N_n$. Inoltre la convergenza è uniforme nei sottoinsiemi compatti di $(0,1)$ e $\rho \mapsto f_{\beta }(\rho )$ è convessa e continua.

Lemma convessità §

Siano ${\Lambda }_1,{\Lambda }_2$ due sottoinsiemi disgiunti ${\Lambda }_1,{\Lambda }_2⋐{\mathbb{Z}}^d$. Se $N_1\le |{\Lambda }_1|$ e $N_2\le |{\Lambda }_2|$ Allora

$$Z_{{\Lambda }_1\cup {\Lambda }_2;\beta ;N_1+N_2}\ge Z_{{\Lambda }_1;\beta ;N_1}{Z}_{{\Lambda }_2;\beta ;N_2}$$

Proof §

$$\sum _{\eta }{e}^{\beta {\sum }_{(i,j)\subset \Lambda }K(i,j)}$$

dove l’insieme delle configurazioni è della forma $\eta \in \{0,1{\}}^{\Lambda }$ con la condizione che $N=\sum {\eta }_i$.

E’ evidente che limitandoci alle configurazioni ${\eta }^{\prime }$ tali che hanno $N_1$ particelle in ${\Lambda }_1$ e $N_2$ in ${\Lambda }_2$. Ottengo una quantità inferiore (sto sommando su meno stati, sempre quantità positive).

Separiamo la somma nell’esponente:

$$\sum _{{\eta }^{\prime }}{e}^{\beta {\sum }_{(i,j)\subset {\Lambda }_1}K(i,j)+\beta {\sum }_{(i,j)\subset {\Lambda }_2}K(i,j)+{\sum }_{i\in {\Lambda }_{1}j\in {\Lambda }_2}\beta K(i,j)}$$

Essendo $K(i,j)\ge 0$ possiamo trascurare il termine di interazione tra le regioni e fattorizzare per ottenere il risultato. $\square$

Lemma “continuità” §

Una sorta di continuità della funzione di partizione rispetto al numero di particelle (i.e. incrementando le particelle di uno la funzione non cambia troppo).

Sia $\Lambda ⋐{\mathbb{Z}}^d$ e $N\in \{0,1,\dots ,|\Lambda |-1\}$. Allora:

$$\frac{|\Lambda |-N}{N+1}{Z}_{\Lambda ;\beta ;N}\le Z_{\Lambda ;\beta ;N+1}\le e^{\beta \kappa }\frac{|\Lambda |-N}{N+1}{Z}_{\Lambda ;\beta ;N}$$

Proof §

Possiamo vedere le configurazioni con $N+1$ particelle come tutte quelle da $N$ particelle a cui poi aggiuniamo un’altra in un sito libero.

$$\sum _{\eta \in \{0,1{\}}^{\Lambda };N(\eta )=N+1}{e}^{-\beta {\mathcal{H}}_K(\eta )}=\frac{1}{N+1}\sum _{\eta \in \{0,1{\}}^{\Lambda };N(\eta )=N}\sum _{{\eta }^{\prime }\ge \eta ;N({\eta }^{\prime })=N+1}{e}^{-\beta {\mathcal{H}}_K({\eta }^{\prime })}$$

è chiaro che $\mathcal{H}({\eta }^{\prime })\le \mathcal{H}(\eta )$, inoltre vale:

$$\mathcal{H}({\eta }^{\prime })=\mathcal{H}(\eta )-k$$

dove $k$ è l’energia dovuta alla nuova particella con quelle già presenti in $\eta$. Sicuramente vale $k\le \kappa$, quindi

$$\mathcal{H}({\eta }^{\prime })\ge \mathcal{H}(\eta )-\kappa$$

Con queste disuguaglianze, e condiserando che ci sono $|\Lambda |-N$ termini nelle somma otteniamo il lemma. $\square$

Proof del limite §

1. esistenza del limite per sequenze particolari di particelle consideriamo la sequenza $N_n=\lceil \rho |{\Lambda }_n|\rceil$ (il ceil). I casi limite $\rho =0$ e $\rho =1$ possono essere calcolati esplicitamente:

$$f_{\beta }(0)=0f_{\beta }(1)=-\frac{\kappa }{2}$$

per i valori intermedi, scriviamo il lemma della continuità come:

$$c^{-1}{Z}_{\Lambda ;N}\le Z_{\Lambda ;N+1}\le c{Z}_{\Lambda ;N}$$

per un qualche $c>1$. Sia $\rho \in (0,1)$. Per tutti i ${\Lambda }_1,{\Lambda }_2$ disgiunti e con ${\Lambda }_1\cup {\Lambda }_2=\Lambda$ abbiamo che $\lceil \rho |\Lambda |\rceil \ge \rho |{\Lambda }_1|+\rho |{\Lambda }_2|\ge \lceil \rho |{\Lambda }_1|\rceil +\lceil \rho |{\Lambda }_2|\rceil -2$, ovvero $N\ge N_1+N_2-2$. Usando due volte verso il basso la precedente disequazione otteniamo:

$$Z_{\Lambda ;\lceil \rho |\Lambda |\rceil }\ge c^{-2}{Z}_{\Lambda ;\lceil \rho |{\Lambda }_1|+\rho |{\Lambda }_2|\rceil -2}$$

adesso consideriamo due volumi disgiunti ${\Lambda }_1,{\Lambda }_2$ con un relativo numero di particelle $N_1=\lceil \rho |{\Lambda }_1|\rceil$ e $N_2=\lceil \rho |{\Lambda }_2|\rceil$. Vale quindi:

$$Z_{\Lambda ;N}\ge c^{-2}{Z}_{{\Lambda }_1;N_1}{Z}_{{\Lambda }_2;N_2}$$

di conseguenza, passando al logaritmo abbiamo una proprietà di subadditività della funzione:

$$a(\Lambda ):=-\log (c^{-2}{Z}_{\Lambda ;\lceil \rho |\Lambda |\rceil })$$

Inoltre, come conseguenza dell’invarianza per traslazione del potenziale di interazione $K$, è anche invariante per traslazione. Possiamo quindi applicare il teorema Limite di successioni subadditive:

$$\underset{n\to \infty }{\lim }\frac{a({\Lambda }_n)}{|{\Lambda }_n|}=\underset{n}{\inf }\frac{a({\Lambda }_n)}{|{\Lambda }_n|}$$

Siccome vale il lower bound

$$f_{\beta ,{\Lambda }_n,N}\ge -\frac{\log 2}{\beta }-\frac{\kappa }{2}$$

quindi esiste l’energia libera, almeno per successioni di $N_n=\lceil \rho |{\Lambda }_n|\rceil$, e con ${\Lambda }_n$ parallelepipedi.

Una conseguenza dell’esistenza, è anche il seguente upper-bound, che segue dal fatto che il limite è pari all’inf:

$$Z_{\Lambda ,\lceil \rho |\Lambda |\rceil }\le c^2{e}^{-\beta f_{\beta }(\rho )|\Lambda |}$$

2. esistenza del limite per sequenze generiche di particelle Assumiamo ora di avere una generica sequenza $N_n$ tale che $\frac{N_n}{|{\Lambda }_n|}\to \rho$. Facciamo vedere che l’errore che si commette è trascurabile nel limite. Applicando la disuguaglianza un numero necessario di volte $|N_n-\lceil \rho |\Lambda |\rceil |$:

$$c^{-|N_n-\lceil \rho |\Lambda |\rceil |}{Z}_{\Lambda ,\lceil \rho |\Lambda |\rceil }\le Z_{\Lambda ;N_n}\le c^{|N_n-\lceil \rho |\Lambda |\rceil |}{Z}_{\Lambda ,\lceil \rho |\Lambda |\rceil }$$

siccome $N_n-\lceil \rho |{\Lambda }_n|\rceil \to 0$, il limite coincide con quello del caso precedente, questo conclude la dimostrazione. $\square$ 3. convergenza uniforme sui compatti di $(0,1)$ Per dimostrare la convergenza uniforme sui compatti di $(0,1)$, sia $I=[a,b]\subset (0,1)$ usiamo la disuguaglianza di continuità con densità in $I$

$$\left|f_{\Lambda \beta ,N+1}-f_{\Lambda \beta ,N}\right|\le \frac{1}{|\Lambda |}\underset{\rho \in I}{\sup }\left\{\kappa +\beta \log \left(\frac{1-\rho }{\rho }\right)\right\}$$

infatti

$$\left|f_{\Lambda \beta ,N+1}-f_{\Lambda \beta ,N}\right|\le -\frac{k}{|\Lambda |}-\frac{1}{\beta |\Lambda |}\underset{N}{\sup }\log \left(\frac{|\Lambda |-N}{N+1}\right)$$ $$\le -\frac{k}{|\Lambda |}-\frac{1}{\beta |\Lambda |}\underset{\rho }{\sup }\log \left(\frac{1-\rho }{\rho }\right)=:C(\beta ,I)$$

quindi possiamo effettuare un bound uniforme per tutte le densità $\rho \in I$, c dunque la convergenza è uniforme, quindi continuità della funzione limite (vedi Lipshitz continuità) in $(0,1)$, usando i lower ed upper bound si mostra che

$$\underset{\rho \downarrow 0}{\lim }{f}_{\beta }(\rho )=0,\underset{\rho \uparrow 1}{\lim }{f}_{\beta }(\rho )=-\frac{\kappa }{2}$$

dunque è continua in tutto $[0,1]$.

La convessità segue dalla quasi convessità e della continuità della funzione limite, infatti considerando sequenze di volumi $D_k=\{0,1,\dots ,2^k{\}}^d$ , $\rho =({\rho }_1+{\rho }_2)/2$

$$Z_{D_{k+1},\lceil \rho |D_{k+1}|\rceil }\ge c^{-2}{\left(Z_{D_k,\lceil {\rho }_1|D_k|\rceil }{Z}_{D_k,\lceil {\rho }_2|D_k|\rceil }\right)}^{2^{d-1}}$$

thus in the limit

$$f_{\beta }(\rho )\le \frac{f_{\beta }({\rho }_1)+f_{\beta }({\rho }_2)}{2}\square$$

Ensemble Gran Canonico §

Ora consentiamo al numero di particelle $N$ di variare, la distribuzione di probabilità diventa:

$${\nu }_{\Lambda ,\beta ,\mu }(\eta ):=\frac{\exp -\beta [\mathcal{H}(\eta )-\mu N(\eta )]}{{\Theta }_{\Lambda ,\beta ,\mu }}$$

la funzione di partizione gran canonica:

$${\Theta }_{\Lambda ,\beta ,\mu }:=\sum _{\eta \in \{0,1{\}}^{\Lambda }}\exp -\beta [\mathcal{H}(\eta )-\mu N(\eta )]$$

fattorizzando e sommando su tutte le configurazioni $\eta$ con $N$ particelle otteniamo la seguente relazione con la funzione di partizione canonica:

$${\Theta }_{\Lambda ,\beta ,\mu }=\sum _{N=0}^{|\Lambda |}{e}^{\beta \mu N}{Z}_{\Lambda ,\beta ,N}$$

Il relativo potenziale termodinamico (intensivo) è la pressione. A volume finito assume la forma:

$$p_{\Lambda ,\beta }(\mu ):=\frac{1}{\beta |\Lambda |}\log {\Theta }_{\Lambda ,\beta ,\mu }\mu \in \mathbb{R}$$

Dalla definizione segue che:

$$\frac{\partial p_{\Lambda ,\beta }}{\partial \mu }=\frac{⟨N⟩}{|\Lambda |}$$

ovvero la densità media. Quindi il potenziale chimico ci permette di controllare il numero di particelle: valori negativi corrispondono ad una fase diluita, positivi grandi ad una fase liquida.

Esistenza della pressione a volume infinito §

Teorema §

Sia ${\Lambda }_n\Uparrow {\mathbb{Z}}^d$ una sequenza nel senso di Van Hove. Per ogni $\mu \in \mathbb{R}$ il limite

$$\underset{n\to \infty }{\lim }{p}_{{\Lambda }_n,\beta }(\mu )=p_{\beta }(\mu )$$

esiste e non dipende dalla scelta delle sequenza ${\Lambda }_n$. $p(\mu )$ è convessa e continua.

Osservazioni §

• Siccome $p_{\beta }(\mu )$ è convessa, la sua derivata:

$${\rho }_{\beta }(\mu ):=\frac{\partial p}{\partial \mu }$$

ovvero la densità media, esiste quasi ovunque. Le derivate destre e sinistre ${\rho }^{+}$ e ${\rho }^{-}$ sono sempre ben definite. Questo permette di scambiare i limite per concludere che se esiste:

$${\rho }_{\beta }(\mu )=\underset{n\to \infty }{\lim }\frac{⟨N_{{\Lambda }_n}⟩}{|{\Lambda }_n|}$$

• $p(\mu )$ è strettamente convessa, ovvero un aumendo di $\mu$ provoca sempre un aumento di densità, infatti derivando:

$$\frac{{\partial }^{2}p}{\partial {\mu }^2}=\frac{\beta }{|\Lambda |}Var(N)$$

Si può dimostrare che $Var(N)>0$, il che implica la stretta convessità.

Per dimostrare l’esistenza del limite, passiamo per l’equivalenza degli ensemble: La pressione è la trasformata di Legendre dell’energia libera, $\mu$ è la variabile coniugata di $N$.

Equivalenza degli ensemble §

Equivalence of ensembles at the level of potentials holds for the general lattice gas. That is, the free energy and pressure are each other’s Legendre transform:

$$f_{\beta }(\rho )=\underset{\mu \in \mathbb{R}}{\sup }\{\mu \rho -p_{\beta }(\mu )\}\forall \rho \in [0,1]$$ $$p_{\beta }(\mu )=\underset{\rho \in [0,1]}{\sup }\{\rho \mu -f_{\beta }(\rho )\}\forall \mu \in \mathbb{R}$$

Dim §

Siccome i termini della somma che definiscono il gran potenziale sono non negativi:

$$\underset{N}{\max }\{e^{\beta \mu N}{Z}_{{\Lambda }_n,\beta ,N}\}\le \sum _{N=0}^{|{\Lambda }_n|}{e}^{\beta \mu N}{Z}_{{\Lambda }_n,\beta ,N}\le (|{\Lambda }_n|+1)\underset{N}{\max }\{e^{\beta \mu N}{Z}_{{\Lambda }_n,\beta ,N}\}$$

Possiamo usare l’upper bound calcolato per l’esisteza dell’energia libera:

$$Z_{\Lambda ,\lceil \rho |\Lambda |\rceil }\le c^2{e}^{-\beta f(\rho )|\Lambda |}$$ $$\underset{N}{\max }\{e^{\beta \mu N}{Z}_{\beta ,{\Lambda }_n,N}\}\le =$$ $$Z_{{\Lambda }_n,\beta ,N}\le c^2\exp \{-\beta [f(\rho )|{\Lambda }_n|+\mu N]\}\le \underset{\rho }{\sup }{c}^2\exp \{-\beta [f(\rho )+\mu \rho ]|{\Lambda }_n|\}$$

quindi per il $\mathrm{limsup}$ vale:

$$\underset{n\to \infty }{\mathrm{limsup}}\frac{1}{\beta |{\Lambda }_n|}\log \Theta \le \underset{\rho }{\sup }\{\mu \rho -f(\rho )\}$$

For the $\mathrm{liminf}$, we use again the fact $f_n\to f$, for any $ϵ>0$ we can find $N$ such that $\forall n\ge N$

$$f_{\beta ,{\Lambda }_n,N_n}-f_{\beta }(\rho )<ϵ$$

this implies for the partition function

$$Z_{\beta ,{\Lambda }_n,N_n}\ge e^{-\beta |{\Lambda }_n|f_{\beta }(\rho )-\beta |{\Lambda }_n|ϵ}$$

this is the trick: let ${\rho }_n\to {\rho }^{\ast }$ be a sequence converging to the $\sup$. Since $\mu \rho -f_{\beta }(\rho$ ) is continuous the values is attained for some ${\rho }^{\ast }$:

$$\mu {\rho }^{\ast }-f_{\beta }({\rho }^{\ast })=\underset{\rho }{\sup }\{\mu \rho -f_{\beta }(\rho )\}$$

Setting $N_n=\lceil {\rho }^{\ast }|{\Lambda }_n|\rceil$ we find that

$$Z_{\beta ,{\Lambda }_n,\lceil {\rho }^{\ast }|{\Lambda }_n|\rceil }\ge e^{-\beta |{\Lambda }_n|f_{\beta }({\rho }^{\ast })-\beta |{\Lambda }_n|ϵ}$$

so that

$$\underset{n}{\mathrm{liminf}}\frac{1}{\beta |{\Lambda }_n|}\log {\Theta }_{\beta ,{\Lambda }_n,\mu }\ge \mu {\rho }^{\ast }-f_{\beta }({\rho }^{\ast })-ϵ=$$

thus the termodinamic limit of the pressure exists. $\square$

Remark (Differentiability of the free energy) The free energy is differentiable everywhere on $(0,1)$. Proof Suppose there exists a point where ${\partial }^{-}f(x)\ne {\partial }^{+}f(x)$, then the pressure would be affine in the interval $[{\partial }^{-}f(x),{\partial }^{+}f(x)]$ by this property of the Legendre transform, but the pressure is strictly convex. $\square$

Gas di sfere due §

Poniamoci nel semplice caso $K(i,j)=0$, ovvero manteniamo solo la parte hard-core del gas. In questo semplice modello i potenziali termodinamici possono essere calcoalti esplicitamente.

The canonical partition function becomes a purely combinatorial quantity, counting the configurations $\eta$ con $N_{\Lambda }(\eta )=N$:

$$Z_{\Lambda ,\beta ,N}=\left(\genfrac{}{}{0ex}{}{|\Lambda |}{N}\right)$$

l’energia libera a volume infinito può essere calcolata approssimando con stirling i fattoriali:

$$f_{\beta }(\rho )=\frac{1}{\beta }\left(\rho \log \rho +(1-\rho )\log (1-\rho )\right)$$

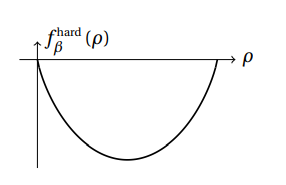
La pressione si può ricavare dalla definizione usando il binomio di Newton:

$$\Theta =\sum _{N=0}^{|\Lambda |}{e}^{\beta \mu N}\left(\genfrac{}{}{0ex}{}{|\Lambda |}{N}\right)=(1+e^{\beta \mu }{)}^{|\Lambda |}$$

quindi:

$$p(\mu )=\frac{1}{\beta }\log (1+e^{\beta \mu })$$

da qui derivando posso calcolare la densità media:

$$\rho (\mu )=\frac{e^{\beta \mu }}{1+e^{\beta \mu }}⟹\mu =\frac{1}{\beta }\log \frac{p}{1-p}$$

Questa espressione è invertibile, quindi posso scrivere il potenziale chimico in funzione della densità per ottenere un’equazione di stato:

$$p=\frac{1}{\beta }\log (1+\frac{p}{1-p})=\frac{1}{\beta }\log (\frac{1}{1-p})=-\frac{1}{\beta }\log (1-p)$$

a basse densità $\log (1-\rho )\simeq -\rho$

$$p=\frac{\rho }{\beta }⟹p=k_{B}T\rho ⟹pv=k_{B}T$$

con $v={\rho }^{-1}=V/N$. Ovvero l’equazione di stato dei gas perfetti.