Turan theorem

What is the maximum size of a graph of order $n$ such that it doesn’t contain an $(r+1)$-clique? Turan’s theorem answer this question.

Turan’s graph §

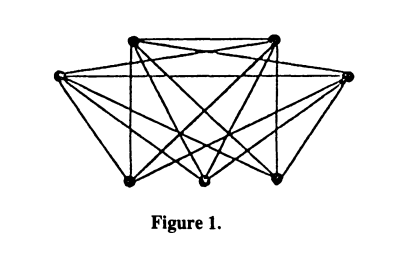
It is easy to see that a complete multipartite graph, where the vertices are partitioned in $r$ subsets of order $n_1,n_2,\dots n_r$, is $r+1$-clique free. Since the total number of edges is

$$\sum _{i\ne j}{n}_i{n}_j$$

it’s clear that we obtain a maximal number of edges if we divide the numbers $n_i$ as evenly as possibile: $|n_i-n_j|\le 1$ for all $i,j$. If $r$ divides $n$, then the number of edges is simply

$$\sum _{i\ne j}\frac{n^2}{r^2}=\left(\genfrac{}{}{0ex}{}{r}{2}\right)\frac{n^2}{r^2}=\frac{r-1}{r}\frac{n^2}{2}$$

Turan’s theorem states that this is the maximum size of all $r+1$-clique free graph of order $n$. For the general case where $n\ne 0$ mod $r$ , the upper bound is corrected by a constant:

$$\left(1-\frac{1}{r}+o(1)\right)\frac{n^2}{2}$$

From now on we will make the assumption that $r|n$, Theorem The maximum size of a graph $G$ of order $n$ that doesn’t contain an $(r+1)$-clique is the size of the turan graph $T(n,r)$:

$$|E(G)|\le \frac{r-1}{r}\frac{n^2}{2}$$

where $T(n,r)$ is the Turan graph, or the complete balanced multipartite graph. Proof Induction on the order of the graph $n$.

• $n=1$ is trivial.
• Suppose now $n>1$. Since our graph has the maxium size such that is $(r+1)$-clique free, it contains $K_r$ (otherwise we could add more edges). Partition the vertices in $G=A\cup B$ where $A$ is the set of vertices of $K_r$. We can bound the maximum number of edges in $G$:

$$|E(G)|\le |E_A|+|E_B|+|E_{AB}|$$

we can compute number of edges in the subgraph induced by $A$, since by definition is $K_2$:

$$|E_A|=\left(\genfrac{}{}{0ex}{}{r}{2}\right)$$

the number of edges across $A$ and $B$ can be bounded by

$$|E_{AB}|\le |B|(r-1)=(n-r)(r-1)$$

since every of the $n-r$ vertices in $B$ can at most be connected to $r-1$ vertices in $A$, otherwise an $r+1$-clique would appear. We can bound $|E_B|$ using the inductive hypotesis, since it has size strictly less than $n$, so

$$|E(G)|\le \left(\genfrac{}{}{0ex}{}{r}{2}\right)+|E(T(n-2,r))|+(n-r)(r-1)$$ $$=\left(\genfrac{}{}{0ex}{}{r}{2}\right)+\frac{r-1}{r}\frac{(n-r{)}^2}{2}+(n-r)(r-1)$$ $$=\frac{r-1}{r}\frac{n^2}{2}\square$$