Teorema di separazione

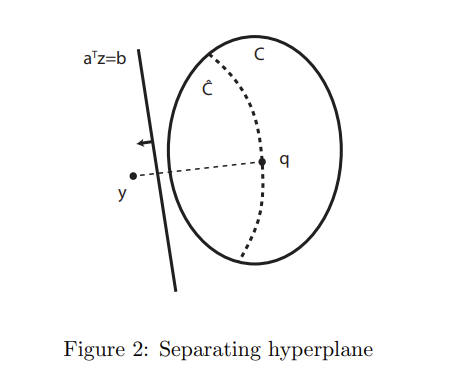
Sia $S\subseteq {\mathbb{R}}^n$ un insieme convesso, chiuso e non vuoto. Sia $y\notin S$, allora esiste un iperpiano definito da $\alpha \ne 0,\alpha \in {\mathbb{R}}^n$, e $b\in \mathbb{R}$ tale che ${\alpha }^{T}y>b$ e ${\alpha }^{T}x<b$ per tutti $x\in S$. Geometricamente:

Dim §

definiamo $f(x)=\frac{1}{2}||x-y|{|}^2$ e $\hat{S}=\{x\in S|||q-y||\ge ||q-x||\}$ avendo fissato un $q\in S$. L’insieme $\hat{S}$ è:

• limitato
• chiuso
• non vuoto (contiene $q$) Possiamo applicare il teorema di Weierstrass della funzione continua $f(x)$, quindi esiste un punto $z$ che minimizza $f$.

Inoltre, per gli $x\in S\setminus \hat{S}$ vale $f(z)\le f(q)<f(x)$, segue dalla definizione della funzione $f$ (gli $x\notin \hat{S}$ sono più lontani da $y$ di $q$). Quindi $z$ è un minimo in tutto $S$. Sia $a=y-z$. Allora $a\ne 0$, siccome $z\in S$ e $y\notin S$ (quindi $z\ne y$). Sia $b=\frac{1}{2}(a^{T}y+a^{T}z)$ Allora:

$$0<a^{T}a=a^T(y-z)=a^{T}y-a^{T}z$$

quindi

$$a^{T}z<a^{T}y⟹2a^{T}z<a^{T}y+a^{T}z=2b⟹a^{T}y>b$$

la prima metà è dimostrata, manca $a^{T}x<b$ per tutti gli $x\in S$, per ora lo abbiamo dimostrato solo per $z$, infatti:

b = \frac{1}{2}(a^Tz + a^Ty) > \frac{1}{2}(2a^Tz) = a^Tz $$Sfruttiamo la convessità di S per far vedere che $a^Tx \leq a^Tz$. Sia $x(\lambda)$ [[Combinazione conica]] di $z$ con un altro elemento $x \in S$. Vale $f(z) \leq f(x(\lambda))$. Quindi:

f(x(\lambda)) = \frac{1}{2}||x(\lambda)-y||^2 = \frac{1}{2}|| \lambda x + (1-\lambda)z - y ||^2 = \frac{1}{2}(\lambda x + (1-\lambda)z - y)^T(\lambda x + (1-\lambda)z - y)

$$Che\grave{e}minoredi:$$

f(z) = \frac{1}{2}(z-y)^T(z-y)

$$portandodal{l}^{\prime }altraparteotteniamo:$$

f(x(\lambda)) - f(z) = \frac{1}{2}(\lambda x + (1-\lambda)z - y)^T(\lambda x + (1-\lambda)z - y) -\frac{1}{2}(z-y)^T(z-y) \geq 0

da qui si ricava (mandando $\lambda \to 0$) che $a^Tz \geq a^Tx$. $QED$