Un approccio numerico per le PDE molto semplice: discretizzare il domnio spaziale e temporale, approssimare le derivate con rapporti di differenze finite.
FD linear advection
Vediamo questo approccio per l’equazione parabolica al prim’ordine linear advection, in . Il primo passo è discretizzare il tempo e lo spazio in punti:
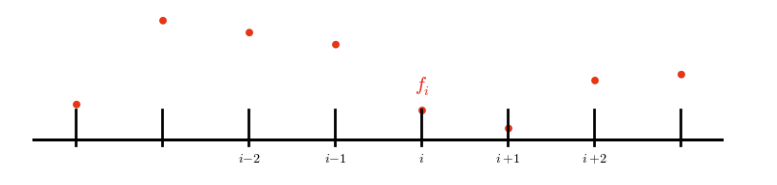 indichiamo con il valore della funzione nel punto spaziale al tempo , fissando una risoluzione spaziale e temporale .
Discretizzando l’equazione otteniamo:
indichiamo con il valore della funzione nel punto spaziale al tempo , fissando una risoluzione spaziale e temporale .
Discretizzando l’equazione otteniamo:
Abbiamo stimato la derivata temporale con Eulero (ordine 1), la derivata spaziale con Verlet (ordine 2 vedi qui).
Esplicitando per il valore al tempo otteniamo:
Il termine costante viene detto number, Courant-Friedrichs-Lewy.
Osservazione 2
quando calcoliamo il valore nel punto 1, “caschiamo fuori”, infatti ci serve il valore nel punto 0: si risolve il problema aggiungendo manualmente dei punti ”ghost points” (stesso problema per l’ultimo punto n). Oppure condizioni di bordo periodiche.
Osservazione 2
Il metodo è instabile! Usiamo la fourier mode analysis per farlo vedere: l’equazione è lineare, quindi ogni modo di fourier non si influenza. Vediamo che succede all’ampiezza di un particolare modo:
Abbiamo usato come unità immaginaria: Calcoliamo il rapporto delle ampiezze per tempi succesivi (usando lo schema numerico):
Il modulo quadro è:
quindi instabile indipendentemente dal valore della costante .