The Hopfield model §

Mattis model (1977) §

Abbiamo studiato il comportamento termodinamico del Modello di Curie-Weiss. In particolare, sotto una certa temperatura critica, il modello arrivava ad uno stato di equilibrio con magnetizzazzione media $\pm 1$ (caso di campo esterno nullo). Di fatto il sistema (visto come rete di neuroni McCulloch-Pitts con rumore) sta “ricordando” uno dei due stati a magnetizzazzione unitaria. E’ facile riadattare le interazioni affinchè la rete converga ad un pattern arbitrario: sia $\xi$ un pattern, l’Hamiltoniana di Mattis

$${\mathcal{H}}^M(\sigma ):=-\frac{1}{2N}\sum _{ij}^N{\xi }_i{\xi }_j{\sigma }_i{\sigma }_j=-\frac{N}{2}{\hat{m}}^2$$

dove abbiamo introdotto la magnetizzazzione di Mattis

$$\hat{m}:=\sum _{i=1}^N{\xi }_i{\sigma }_i$$

A livello matematico il modello è identico a quello di Curie-Weiss, ed al di sotto della temperatura critica il sistema ha come configurazione di equilibrio gli stati con $\hat{m}=\pm 1$, ovvero $\pm \xi$.

Notiamo che abbiamo usato la regola di Hebb per definire le interazioni.

Low load §

Studiamo il caso di numero di pattern finito, detto basso carico. Le interazioni sono definite in accordo con la regola di Hebb

$$J_{ij}=\frac{1}{N}\sum _{\mu =1}^P{\xi }_i^{\mu }{\xi }_j^{\mu }$$

e con pattern Rademacher.

L’hamiltoniana del sistema è

$$\mathcal{H}(\sigma )=-\frac{1}{N}\sum _{i<j}\sum _{\mu }{\xi }_i^{\mu }{\xi }_j^{\mu }{\sigma }_i{\sigma }_j=-\frac{1}{2N}\sum _{ij}\sum _{\mu }{\xi }_i^{\mu }{\xi }_j^{\mu }{\sigma }_i{\sigma }_j+\frac{1}{2N}\sum _i\sum _{\mu }({\xi }_i^{\mu }{)}^2{\sigma }_i^2$$ $$=-\frac{N}{2}\sum _{\mu }{\hat{m}}_{\mu }^2+\frac{P}{2}$$

ovviamente il termine costante è ininfluente nel limite termodinamico. Calcoliamo la funzione di partizione dipendente da una specifica realizzazzione dei $P$ pattern rademacher.

$$Z_{N,\beta ,\xi }=\sum _{\sigma }\exp \left(\frac{\beta }{2N}\sum _{i,j,\mu }{\xi }_j^{\mu }{\xi }_i^{\mu }{\sigma }_i{\sigma }_j\right)$$

un trucco per svolgere questo conto è introdurre una densità degli stati continua

$$Z={\int }_{-\infty }^{+\infty }z(m)dm$$

ovviamente siccome le magnetizzazzioni di mattis $m_{\mu }$ hanno solo alcuni valori razionali tra $-1$ ed $1$, dovremmo intrdurre delle delta, che rappresenteremo come la loro trasformata

$$\delta (x-y)=\frac{1}{2\pi }\int e^{iz(x-y)}dz$$

quindi

$$Z_{N,\beta ,\xi }=\sum _{\sigma }\int \left[{\Pi }_{\mu =1}^{P}d{m}_{\mu }\delta (m_{\mu }-\frac{1}{N}\sum _i{\xi }_i^{\mu }{\sigma }_i)\right]\exp \left(\frac{\beta N}{2}\sum _{\mu }{m}_{\mu }^2\right)$$ $$=\frac{1}{2\pi }\sum _{\sigma }\iint \left[{\Pi }_{\mu =1}^{P}d{m}_{\mu }d{\hat{m}}_{\mu }\exp i{\hat{m}}_{\mu }(m_{\mu }-\frac{1}{N}\sum _i{\xi }_i^{\mu }{\sigma }_i)\right]\exp \left(\frac{\beta N}{2}\sum _{\mu }{m}_{\mu }^2\right)$$ $$=\frac{1}{2\pi }\sum _{\sigma }\iint \left[{\Pi }_{\mu =1}^{P}d{m}_{\mu }d{\hat{m}}_{\mu }\right]\exp \left[]\sum _{\mu }i{\hat{m}}_{\mu }(m_{\mu }-\frac{1}{N}\sum _i{\xi }_i^{\mu }{\sigma }_i)+\frac{\beta N}{2}\sum _{\mu }{m}_{\mu }^2\right]$$

usando l’integrale di picco prima per l’integrale sulle $d{\hat{m}}_{\mu }$ e dopo sulle $d{m}_{\mu }$ i termini di ordine $N$ che sopravvivono dell’energia libera intensiva del limite termodinamico sono

$$⟨f{⟩}^Q=\underset{m}{\min }\left\{\frac{1}{2}\sum _{\mu }{m}_{\mu }^2-\frac{1}{\beta }\mathbb{E}\log 2\cosh (\beta \sum _{\mu }{m}_{\mu }{\xi }_i^{\mu })\right\}$$

dove le magnetizzazzioni di mattis soddisfano l’equazione di autoconsistenza

$$m_{\mu }=\mathbb{E}\sum _i{\xi }_i^{\mu }\tanh (\beta \sum _{\nu }{m}_{\nu }{\xi }^{\nu })$$

il valore atteso è su ${\xi }^{\mu }$ Rademacher.

Studiamo il caso di pattern puro, ovvero $m_1\ne 0$ mentre tutte le altre magnetizzazzioni di mattis sono nulle. L’equazione di autoconsistenza diventa semplice da analizzare, infatti

$$m_1=\tanh \beta m_1$$

dove abbiamo soppresso $\xi$ date che la tangente iperbolica è dispari. Abbiamo ottenuto proprio l’equazione di autoconsistenza del Modello di Curie-Weiss.

L’analisi della stabilità suegue direttamente da Curie-Weiss, avremo quindi una regione di retrivial (fase ferromagnetifca) ed una caotica (paramagnetica).

Osservando che la derivata è proprio $\beta$, sappiamo che il valore critico ${\beta }_c=1$.

Si possono poi studiare gli stati detti misture simmetriche, ovvero il vettore delle magnetizzazzioni di mattis è $\mathbf{m}=m_n(1,1,1,\dots ,0,0,\dots )$ non nullo per $n$ pattern, e con stesso valore di overlap.

Scrivendo in forma vettoriale le equazioni di autoconsistenza

$$\mathbf{m}=\mathbb{E}\xi \tanh (\beta \xi \cdot \mathbf{m})$$

per ogni termine

$$m_n=\frac{1}{n}\mathbb{E}\sum _{\mu =1}^n{\xi }^{\mu }\tanh (\beta m_n\sum _{\mu =1}^n{\xi }^{\mu })$$

definendo le somme parziali $z_n:={\sum }_{\mu =1}^n{\xi }^{\mu }$

Possiamo studiare analiticamente il caso noiseless $\beta \to \infty$ (la tangente iperbolica vale uno)

$$m_n=\frac{1}{n}\mathbb{E}[|z_n|]$$

La conclusione è che stati misti simmetrici dispari sono stabili (minimi dell’eneregia libera), mentre gli stati pari sono instabili (punti di sella).

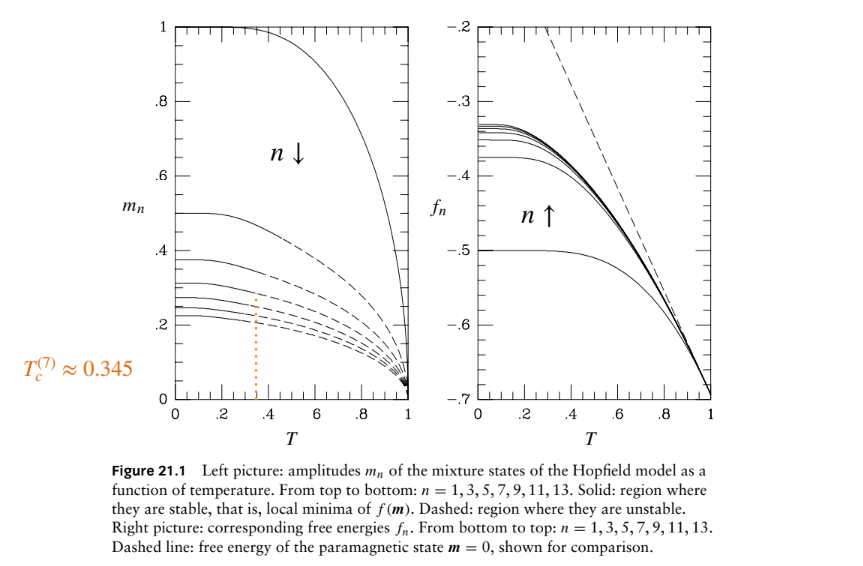
Se la temperatura è abbastanza alta (ma sempre nella regione di retrival) gli stati misti diventano instabili (nice!) ma il recupero degli stati puri perde qualità ;(.

Signal-to-noise analysis §

Analisi euristica per stimare la stabilità dei pattern, vale sia per il caso a basso carico che alto.

Se vogliamo che uno dato pattern sia stabile (nella dinamica deterministica) deve valere

$${\sigma }_i(t+1)=sign({\phi }_i(\sigma (t)))={\sigma }_i(t)$$

Esplicitiamo il campo locale quando $\sigma ={\xi }^1$

$${\xi }_i^1{\phi }_i({\xi }^1)=\frac{1}{N}\sum _{j\ne i}\sum _{\mu }{\xi }_i^1{\xi }_i^{\mu }{\xi }_j^{\mu }{\xi }_j^1>0$$

se devono avere lo stesso segno il prodotto deve essere maggiore di zero. separando il termine $\mu =1$

$${\xi }_i^1{\phi }_i({\xi }^1)=\frac{N-1}{N}+\frac{1}{N}\sum _{j\ne i}\sum _{\mu =2}^P{\xi }_i^1{\xi }_i^{\mu }{\xi }_j^{\mu }{\xi }_j^1$$

Nel limite termodinamico $N\to \infty$ il primo termine tende ad uno, e viene detto termine di segnale. Il restante è detto termine di rumore.

$${\xi }_i^1{\phi }_i({\xi }^1)=1+R$$

assumendo indipendenti le $\xi$, il termine di rumore è composto da $\simeq N\times P$ termini $\pm 1$. Sempre per $N$ grandi sarà distribuito come una gaussiana di varianza $\sqrt{NP}$, dunque alla fine

$$R\approx \sqrt{\frac{P}{N}}$$

questa analisi rudimentale ci dice che se il numero di pattern cresce più lentamente rispetto ad $N$, tutti i pattern sono stabili (anche il rumore tende a zero).

Consideriamo una $3$-mistura simmetrica. ${\sigma }_i:=sgn({\xi }_i^1+{\xi }_i^2+{\xi }_i^3)$. Se calcoliamo la magnetizzazzione di mattis di uno dei tre stati con questa mistura

$$m_{\nu }^{(3)}=\frac{1}{N}\sum _i^{N}sgn({\xi }_i^1+{\xi }_i^2+{\xi }_i^3){\xi }_i^{\nu }$$

La media empirica ($N>>1$) converge al valore atteso

$$=\mathbb{E}[sgn({\xi }_i^1+{\xi }_i^2+{\xi }_i^3){\xi }_i^{\nu }]=0.5\nu =1,2,3$$

mentre è nulla per $\nu >3$.

Controlliamo la stabilità

$${\sigma }_i^{(3)}{\phi }_i({\sigma }^{(3)})=S+R$$ $$S={\sigma }_i^{(3)}\sum _{\mu =1}^3{m}_{\nu }^{(3)}{\xi }_i^{\mu }=0.5sgn({\xi }_i^1+{\xi }_i^2+{\xi }_i^3)({\xi }_i^1+{\xi }_i^2+{\xi }_i^3)=0.5|{\xi }_i^1+{\xi }_i^2+{\xi }_i^3|$$ $$R=\frac{1}{N}\sum _{j=1}^N\sum _{\mu =4}^P{\sigma }_i^{(3)}{\xi }_i^{\mu }{\xi }_j^{\mu }{\sigma }_j^{(3)}$$

per il termine di rumore vale la stessa analisi del caso puro, ho una somma di circa $NP$ termini $\pm 1$, dunque il termine di rumore è del tipo

$$R\approx \sqrt{\frac{P}{N}}$$

Analizziamo la stabilità dei pattern puri nel caso ad alto carico. E’ chiaro che se $P=\alpha N$, il termine di rumore nel limite $N\to \infty$ converge ad una gaussiana non varianza non nulla:

$$R\to N(0,\alpha )$$

Quindi la probabilità che un sito sia stabile è la probabilità che

$$\mathbb{P}(R>-1)$$

probabilità esprimibile in termine della cumulativa, ovvero la $erf(x)$. Se assumiamo $\alpha <<1$ possiamo usare l’espressione approssimata ed ottenere

$$\mathbb{P}(R>-1)\approx 1-\sqrt{\frac{\alpha }{2\pi }}{e}^{-\frac{1}{2\alpha }}$$

Affinchè lo stato sia stabile, tutti gli $N$ siti lo dovranno essere. Assumendo indipendenza la proabilità che uno stato puro sia stabile diventa

$$\mathbb{P}(\xi \text{ stabile })={\left(1-\sqrt{\frac{\alpha }{2\pi }}{e}^{-\frac{1}{2\alpha }}\right)}^N\approx 1-N\sqrt{\frac{\alpha }{2\pi }}{e}^{-\frac{1}{2\alpha }}$$

l’evento complentare è la probabilità di avere degli errori, quindi il valore atteso di errori $N_{err}$ sarà

$$N_{err}=N\sqrt{\frac{\alpha }{2\pi }}{e}^{-\frac{1}{2\alpha }}<<1$$

vogliamo siano molto minori di uno. Possiamo risolvere per $\alpha$ ed ottenere

$$P_c=\frac{N}{2\log N}$$

se richiediamo la stabilità di tutti i pattern ($PN$ siti)

$$P_c=\frac{N}{4\log N}$$

notiamo che questi casi sono sempre in basso carico, ovvero $P/N\to 0$.

High load §