Metodo di Gauss MEG

Eliminazione Gaussiana MEG §

Per risolvere un sistema lineare con questo metodo occorrono $2/3n^3$ $flops$, a cui vanno aggiunti $2n^2$ $flops$ per risolverte i due sistemi triangolari.

L’idea è ridurre il generico sistema $Ax=b$ ad un sistema equivalente (stesse soluzioni) $Ux=d$ ma con $U$ matrice triangolare superiore. Una volta fatto ciò basta usare backward substitution ed in $n^2$ FLOPS si ha la soluzione.

Applicheremo al sistema $(A,b)$ trasformazioni che mantengono equivalente il sistema, sostituendo una riga con una combinazione lineare di altre righe per ottenere delle cancellazioni.

Sia $A\in {\mathbb{R}}^{n\times n}$ non singolare. Supponiamo che il primo elemento diagonale $a_{11}\ne 0$, allora definisco dei moltiplicatori:

$$m_{i1}=\frac{a_{i1}}{a_{11}}i=1,\dots ,n$$

fisso la prima colonna, ottengo un vettore di coefficienti che mi permette di azzerare tutti gli elementi sotto $a_{11}$.

Definisco un nuovo sistema $(A^{(2)},b^{(2)})$ equivalente:

$$\begin{array}{rl}& a_{ij}^{(2)}=a_{ij}^{(1)}-m_{i1}{a}_{1j}^{(1)}i,j=2,\dots ,n\\ & b_i^{(2)}=b_i^{(1)}-m_{i1}{b}_1^{(1)}\end{array}$$

Il nuovo sistema equivalente avrà la forma

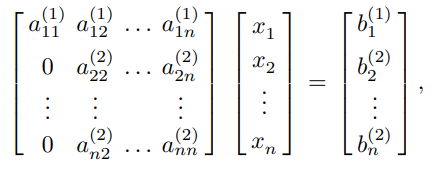
Continuo, in generale al passo $k$ voglio che $a_{kk}^{(k)}\ne 0$. Quando $k=n$, avrò un sistema triangolare superiore.

Per portare a termine l’eliminazione di Gauss servono $2(n-1)n(n+1)/3+n(n-1)$ FLOPS, cui vanno aggiunti $n^2$ FLOPS per risolvere il sistema triangolare. Servono dunque circa $(2n^3/3+2n^2)$ FLOPS per risolvere il sistema lineare attraverso il MEG, trascurando i termini di ordine inferiore, si può dire che il processo di eliminazione gaussiana costa $2n^3/3$ FLOPS.

Affinchè il MEG possa terminare regolarmente, gli elementi pivotali a^{(k)}_{kk}$$ , con k = 1,…,n − 1$, devono essere non nulli. Purtroppo il solo fatto che gli elementi diagonali di A siano tutti diversi da zero, non è sufficiente ad impedire l’eventuale creazione di elementi pivotali nulli durante il processo di eliminazione.

Servono condizioni più forti per garantire che MEG termini.