Fattorizzazione di Cholesky

Fattorizzazione di Cholesky $A=H^{T}H$ §

Teorema Sia $A\in {\mathbb{C}}^{n\times n}$ una matrice hermitiana definita positiva. Allora esiste un’unica matrice triangolare superiore $H$ tale che $A=H^{T}H$. La matrice $H$ è definita come, per $j=2,\dots ,n$:

$$\begin{array}{rl}& h_{11}=\sqrt{a_{11}}\\ & h_{ij}=\frac{a_{i}j-{\sum }_{k=1}^{i-1}{h}_{ki}{h}_{kj}}{h_{ii}}i=1,\dots j-1\\ & h_{jj}={\left(a_{jj}-\sum _{k=1}^{j-1}{h}_{kj}^2\right)}^{1/2}\end{array}$$

Dimostrazione

Procediamo per induzione rispetto alla dimensione $j$ della matrice $A_j\in {\mathbb{C}}^{j\times j}$ hermitiana (se una matrice è hermitiana anche tutte le sue sottomatrici principali lo sono).

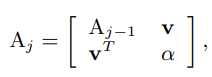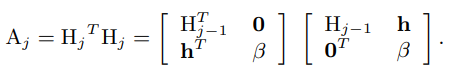Per $J=1$ è vero, infatti $h_{11}=\sqrt{a_{11}}$ . Supponiamo valga per $j-1$ con $j\ge 2$, ovvero esista $H_{j-1}$ triangolare superiore tale che $A_{j-1}=H_{j-1}^T{H}_{j-1}$, facciamo vedere che vale anche per $j$. Partizioniamo $A_j$ nel modo seguente: Con $\alpha \in \mathbb{R}$. Cerchiamo una fattorizzazione della forma: con $\beta \in \mathbb{R}$. Svolgendo il prodotto ed imponendo l’uguaglianza con gli elmenti di $A_j$ si ottengono le equazioni:

$$\{\begin{array}{l}{H}_{j-1}^{H}h=v\\ \\ h^{H}h+{\beta }^2=\alpha \end{array}$$

Trovare una fattorizzazione per $A_j$ equivale a trovare il vettore $h$ e il numero reale $\beta$. Il vettore $h$ esiste ed è univocamente determinato, siccome $H_{j-1}^H$ è non singolare. Dopo di che dobbiamo verificare che

$$\beta ={\sqrt{\alpha -\Vert h\Vert }}^2\in \mathbb{R}$$

si fa vedere calcolando il determinante di $A_j$, che non è singolare:

$$0<det(A_j)=det(H_j^H)det(H_j)={\beta }^{2}det(H_{j-1}{)}^2={\beta }^2$$

quindi $\beta$ è reale. $\square$

Costo computazionale §

https://math.stackexchange.com/questions/217738/how-to-calculate-the-cost-of-cholesky-decomposition

$$\frac{1}{3}{n}^3+O(n^2)$$