Alberi §

Vediamo una caratterizzazione completa di questi grafi.

Def (Foresta) Un grafo $G$ acicliclo viene detto foresta. Def Un grafo $G$ viene detto albero se è una foresta ed è connesso.

In effetti una foresta è un’unione disgiunta di alberi.

Teorema Un grafo $G$ è una foresta se e solo se per ogni coppia di vertici $x,y$ esiste al più un solo cammino.

Dim Se $G$ contiene un ciclo (non è una foresta), allora scelti due vertici che compaiono nel ciclo, esistono due cammini che li collegano. Analogamente, siano $x_0,x_1,\dots ,x_l$ e $x_0,y_1,\dots x_l$ due cammini distinti tra i vertici $x_0,x_l$. Sia $i$ il primo indice dove sono distinti, ovvero $x_i\ne y_i$, sia $j$ l’ultimo indice $j\ge i$ tale che $x_j=y_j$ (deve esistere, sicuramente vale per l’ultimo vertice essendo $x_l$ in emtrambi i cammini). Allora ottengo il ciclo:

$$x_{i-1},x_i,\dots x_j,y_{j-1},\dots ,y_i,y_{i-1}$$

quindi $G$ non è una foresta. $\square$

Caratterizzazione degli alberi §

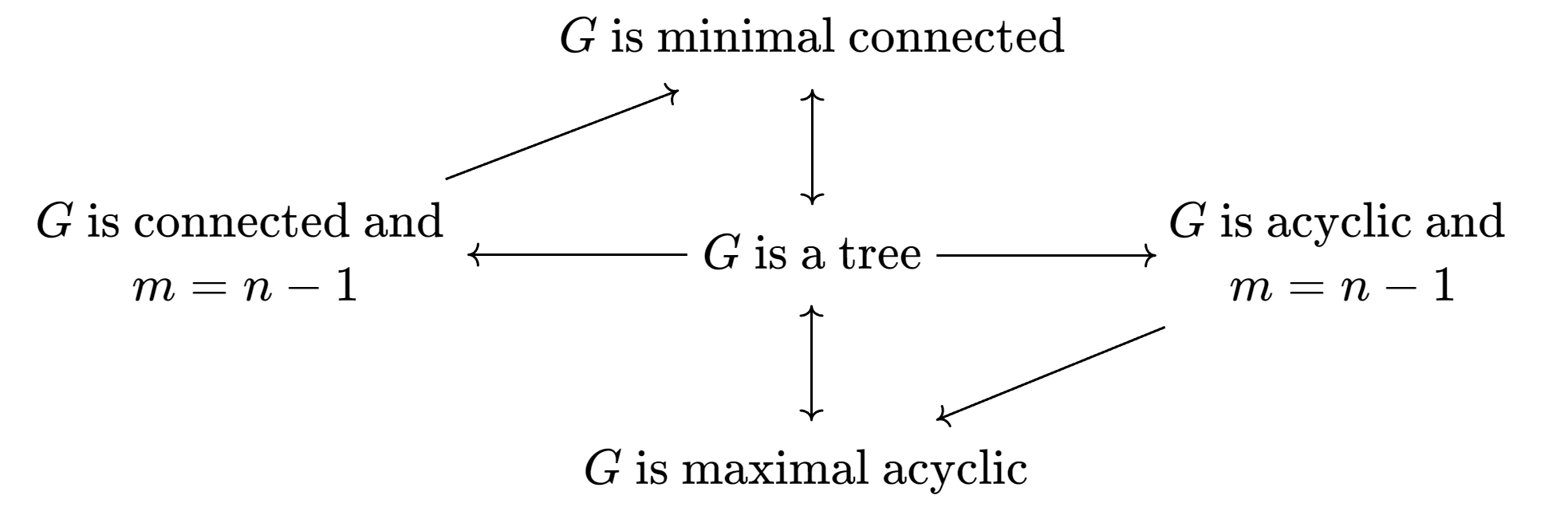
Le seguenti condizioni sono equivalenti:

1. $G$ è un albero.
2. Esiste uno e un solo cammino tra ogni coppia di vertici.
3. $G$ è un grafo minimale connesso: se tolto anche un solo arco, diventa sconnesso (ogni arco è un ponte).
4. $G$ è un grafo massimale aciclico: se aggiungo anche un solo arco, si crea un ciclo.
5. $G$ è aciclico e vale $|V(G)|=|E(G)|-1$.
6. $G$ è connesso e vale $|V(G)|=|E(G)|-1$.

Dim

• $(1⟹2)$ Esiste almeno un cammino siccome $G$ è connesso. Se per assurdo ne esistessero più di uno, allora ho un ciclo.
• $(2⟹3)$ Sia $xy\in E(G)$. Il grafo $G\setminus xy$ non può contenere nessun cammino tra $x$ ed $y$. Quindi $G$ è disconnesso e $G$ è un grafo connesso minimale.
• $(2⟹4)$ In maniera analoga, se $xy\notin E(G)$, allora nel grafo $G\cup xy$ ottengo due cammini tra $x$ ed $y$, quindi un ciclo e $G$ è un grafo aciclico massimale.
• $(3⟹1)$ Supponiamo $G$ sia un grafo connesso minimale, per far vedere che è un albero basta verificare sia aciclico. Supponiamo per assurdo contenga un ciclo $x,z_1,z_2,\dots ,y$ e $xy\in E(G)$, allora esistono due cammini tra i vertici $x$ ed $y$, posso rimuovere $xy$ da $G$ e rimanere connesso, contro l’ipotesi di minimalità.
• $(4⟹1)$ Supponiamo $G$ sia aciclico massimale, basta far vedere che $G$ è anche connesso per dimostrare che è un albero. Se per assurdo non fosse connesso, siano $x$ ed $y$ vertici in differenti componenti connesse del grafo, aggiungere l’arco $xy$ non crea cicli, contro l’ipotesi di massimalità.$\square$
• $(1⟹5)$ Segue banalmente dal lemma aciclico.
• $(1⟹6)$ Segue banalmente dal lemma connesso
• $(5⟹1)$ Facciamo vedere per induzione sull’ordine che se vale la relazione ed è aciclico, allora $G$ è un albero. Base induttiva $n=1$: triviale, la relazione è soddisfatta e il grafo è un albero. Passo induttivo: supponiamo che un grafo $G$ di ordine $n$ soddisfi $m=n-1$. Siccome è aciclico, esiste almeno un vertice $v$ di grado $1$. Costruisco un sottografo $H$ rimuovendo questo vertice. Siccome ho tolto un vertice ed un arco, $H$ continua a soddisfare la relazione di eulero, e continua banalmente ad essere aciclico. Per ipotesi induttiva, $H$ è un albero. Ma allora anche $G$ lo è, infatti era aciclico per ipotesi, ed è connesso.
• $(5⟹4)$ Banalmente dal lemma aciclico, se aggiungo un arco $m=n$, quindi ha un ciclo.
• $(6⟹3)$ Banalmente dal lemma di connessione, se tolgo un arco qualuque da $G$, allora avrà $m=n-2$ archi e sarà disconnesso.

RECAP connesso implica almeno $n-1$ archi, aciclico implica al massimo $n-1$ archi, quindi un albero (connesso ed aciclico) deve avere esattamente $n-1$ archi. Se un grafo connesso ha $n-1$ archi, è un albero: è connesso minimale. Un grafo aciclico e con $n-1$ archi è un albero: è aciclico massimale.

Corollario Un grafo $G$ è una foresta se e solo se vale la relazione:

$$|E(G)|=|V(G)|-\lambda (G)$$

dove $\lambda (G)$ è il numero di componenti connessi del grafo. Dim Segue banalmente dal fatto che una foresta è un’unione disgiunta di alberi. $\square$

Cool facts about trees §

Proposition The average degree $ad$ defined as

$$ad:=\frac{{\sum }_{v\in V}d(v)}{|V|}$$

in a tree uniquely determines the order of the graph.

Proof We use Handshake Lemma, and the $m=n-1$ identity

$$ad=\frac{2|E|}{|V|}=\frac{2|V|-2}{|V|}$$

solving for $|V|$ we get the formula

$$|V|=\frac{1}{1-\frac{ad}{2}}ad=2-\frac{2}{|V|}$$

from this formula we gather another cool fact: in a tree the average degree is strictly less than $2$:

$$ad<2$$

The path graph $P_n$, which is a tree, in the limit $n\to \infty$ tends to $ad=2$. $\square$

Proposition In a tree the number of leaves is

$$\#leaves=2+\sum _{d(v_i)\ge 3}[d(v_i)-2]$$

where the sum is taken over vertices of degree at least $3$. Proof By induction, need to check $3$ cases. $\square$