Fattorizzazione LU §

Mostreremo come il Metodo di Gauss MEG equivalga a fattorizzare la matrice $A$ di partenza nel prodotto di due matrici, $A=LU$. Il vantaggio di questo punto di vista è che posso sfruttare la stessa fattorizzazione per risolvere sistemi con termine noto $b$ diverso:

$$LUx=b\{\begin{array}{l}Ly=b\\ Ux=y\end{array}$$

e posso risolvere i due sistemi triangolari con gli algoritmi backward e forward.

L’osservazione chiave è che possiamo scrivere la nuova matrice $A^{(k+1)}$ come prodotto di una matrice dei moltiplicatori con quella precedente $A^{(k+1)}=M^{(k)}{A}^{(k)}$

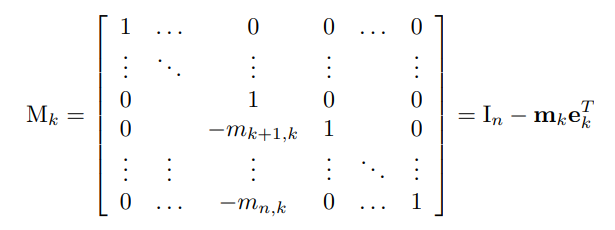
Di conseguenza:

$$U=M^{(n-1)}\dots M^{(1)}A$$

quindi la matrice cercata $L$ sarà:

$$L=(M^{(n-1)}\dots M^{(1)}{)}^{-1}={M^{(1)}}^{-1}\dots {M^{(n-1)}}^{-1}$$

Calcolare le inverse delle matrici $M^{(k)}$ è semplice:

$${M^{(k)}}^{-1}=(Id-m_k{e}_k^T{)}^{-1}=Id+m_k{e}_k^T$$

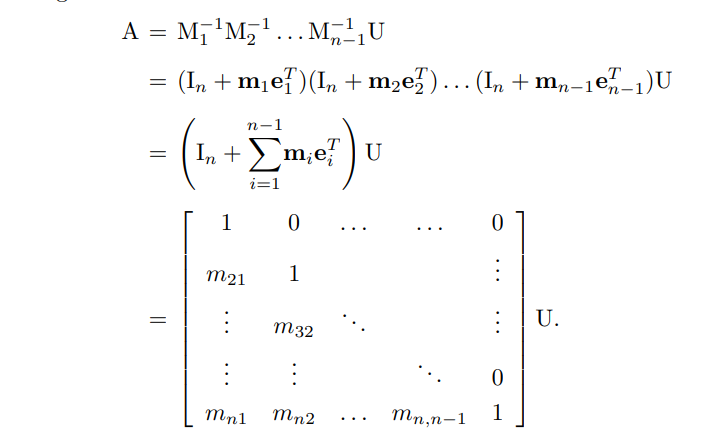
Proposizione §

Sia $A\in {\mathbb{R}}^{n\times n}$. La fattorizzazione $A=LU$ con $l_{ii}=1$ con $i=1,\dots ,n$, esiste ed è unica se e solo se le sottomatrici principali $A_i$ di ordine $i=1,\dots ,n-1$ sono non singolari.

Matrici $A$ che soddisfano questo prerequisito sono matrici definite positive

Generalizzazione PA=LU §

La fattorizzazione può essere generalizzata cercando, al passo $k$ del processo di eliminazione, un elemento pivotale non nullo scorrendo gli elementi della sola sottocolonna. Per tale motivo essa è detta pivotazione parziale (per righe). Un valore grande di $m_{ik}$ (generato ad esempio da un valore piccolo del pivot $a_{kk}$ può amplificare gli eventuali errori di arrotondamento. Per questo motivo si sceglie come elemento pivotale l’elemento di modulo massimo della colonna e la pivotazione parziale viene generalmente operata ad ogni passaggio anche quando non si incontrano elementi pivotali nulli.

Fattorizzazzione LU per matrici a banda §

Se la nostra matrice quadrata $A$ ha una struttura a banda, ovvero e non nulla solo sulla diagonale e le $p$ sottodiagonali e $q$ sopradiagonali, è evidente che possiamo solvegere la fattorizzazione in meno $flops$,

Calcolo dell’inversa §

Trovare l’inversa di una matrice invertibile $A$ equivale a trovare la matrice $X$ tale che:

$$AX=I$$

ma questo è equivalente a risolvere $n$ sistemi lineari del tipo:

$$A{X}_i=e_i$$

dove $X_i$ è la $i$-esima colonna di $X$. Possiamo risovlere questi sistemi usando la fattorizzazione LU di A, per un costo totale di:

$$\frac{2}{3}{n}^3+n(2n^2)=\frac{8}{3}{n}^3=\Theta (n^3)$$

Stabilità §

Nel caso con pivoting parziale per righe, scegliendo come pivot l’elementod i modulo massimo, vale il seguente risultato di stabilità:

$$\underset{ij}{\max }|l_{ij}|\le 1$$

Inoltre vale per la matrice $U$

$$\underset{ij}{\max }|u_{ij}|\le {\rho }_n\underset{ij}{\max }|a_{ij}|$$

dove ${\rho }_n$ generalmente è una costante $O(1)$, tuttavia esistono esempi in cui ${\rho }_n=2^{n-1}$. Questo tipo di stabilità che dipende dalla dimensione viene detta in senso debole.