The Ising model

Finite volume pressure §

Infinite volume pressure §

Proposition In the thermodynamic limit the pressure

$$\psi (\beta ,h):=\underset{{\Lambda }_n\uparrow {\mathbb{Z}}^d}{\lim }\frac{1}{|{\Lambda }_n|}\log Z_{{\Lambda }_n}^{\#}(\beta ,h)$$

is well defined, indipendent of the sequence ${\Lambda }_n$ and the boundary conditions. Moreover $\psi$ is convex in ${\mathbb{R}}_{\ge 0}\times \mathbb{R}$ and symmetric in $h$ (like the finite volume pressure).

Proof

1. A new Hamiltonian $\overline{\mathcal{H}}$ First a trick to ensure that the interaction energy across boudaries is always positive: writing $({\omega }_i{\omega }_j-1)+1$ in the Hamiltonian one can write

$${\mathcal{H}}_{\Lambda ,\beta ,h}^{\#}(\omega )={\overline{\mathcal{H}}}_{\Lambda ,\beta ,h}^{\#}(\omega )-\beta |E_{\Lambda }|$$

Let ${\Lambda }_1\cap {\Lambda }_2=\varnothing$, then

$${\overline{\mathcal{H}}}_{{\Lambda }_1\cup {\Lambda }_2}(\omega )={\overline{\mathcal{H}}}_{{\Lambda }_1}(\omega )+{\overline{\mathcal{H}}}_{{\Lambda }_2}(\omega )+R$$

where the interaction energy $R$ is

$$R=-\beta \sum _{i\sim ji\in {\Lambda }_{1}j\in {\Lambda }_2}({\omega }_i{\omega }_j-1)\ge 0$$

so that

$${\overline{\mathcal{H}}}_{{\Lambda }_1\cup {\Lambda }_2}(\omega )\ge {\overline{\mathcal{H}}}_{{\Lambda }_1}(\omega )+{\overline{\mathcal{H}}}_{{\Lambda }_2}(\omega )$$

but this implies that the partition function is submultiplicative (it’s also translation invariant by definition):

$${\overline{Z}}_{{\Lambda }_1\cup {\Lambda }_2}\le {\overline{Z}}_{{\Lambda }_1}{\overline{Z}}_{{\Lambda }_2}$$

2. Existence of the limit for sequences of boxes $\mathcal{R}$ so that the pressure is subadditive. Using Fekete’s lemma we know that the following limit exists:

$$\underset{n\to \infty }{\lim }\frac{1}{|{\Lambda }_n|}\log {\overline{Z}}_{{\Lambda }_n,\beta ,h}=\underset{n}{\inf }\frac{1}{|{\Lambda }_n|}\log {\overline{Z}}_{{\Lambda }_n,\beta ,h}$$

also since $\overline{\mathcal{H}}\le -\beta (-2|E_{\Lambda }|)+|h||\Lambda |$ we can bound from below the partition function

$${\overline{Z}}_{\Lambda ,\beta ,h}\ge e^{\ln 2|\Lambda |+2\beta |E_{\Lambda }|+|h||\Lambda |}$$

and the pressure

$$\frac{1}{|{\Lambda }_n|}\log {\overline{Z}}_{{\Lambda }_n,\beta ,h}\ge \ln 2+|h|+2\beta \frac{|E_{{\Lambda }_n}|}{|{\Lambda }_n|}\ge Const.$$

note that the number of edges is bounded for example by $d|\Lambda |$ (view the lattice a a graph and use the Handshake Lemma). So the $\inf$ is a finite number, and the limit exists.

Now the existence of this limit implies the existence of the pressure, since they differ by a term

$$\underset{n\to \infty }{\lim }\frac{1}{|{\Lambda }_n|}\log Z_{{\Lambda }_n,\beta ,h}=\underset{n\to \infty }{\lim }\frac{1}{|{\Lambda }_n|}\log {\overline{Z}}_{{\Lambda }_n,\beta ,h}-\beta \frac{|E_{{\Lambda }_n}|}{|{\Lambda }_n|}$$

the last term (which also has a limit since we can apply Feket’s lemma) can be computed and is equal to

$$\underset{n\to \infty }{\lim }\frac{|E_{{\Lambda }_n}|}{|{\Lambda }_n|}=d$$

So we have proven the existence of the pressure for any sequences of rectangles that converges to ${\mathbb{Z}}^d$.

3. estenzione a sequenze di volumi nel senso di Van Hove To extend this result to any sequence ${\Lambda }_n\uparrow {\mathbb{Z}}^d$ in the sense of Van Hove, the idea it to approximate any volumes by rectangles, the Van Hove condition ensures that in the limit the difference goes to zero.

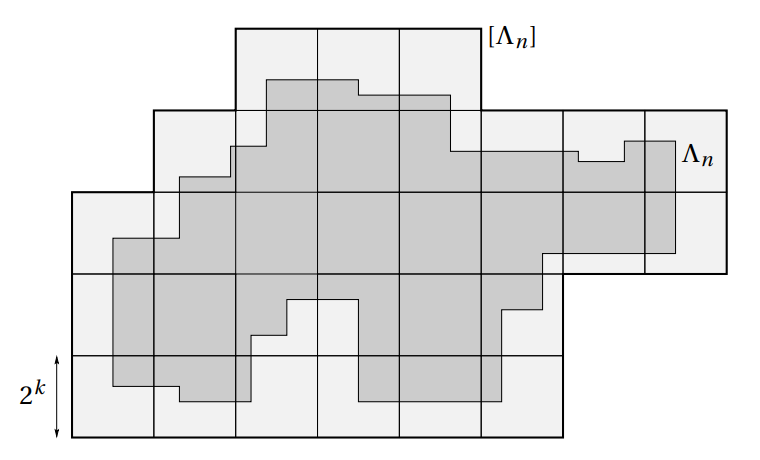
Consider the simple sequence of cubes $B_n=\{-n,\dots ,n{\}}^d$. Since this is a sequence of rectangles such that $B_n\uparrow {\mathbb{Z}}^d$, we now that the limit

$$\underset{n\to \infty }{\lim }\frac{1}{|B_n|}\log Z_{B_n,\beta ,h}=\psi (\beta ,h)$$

We now decompose a generic volume ${\Lambda }_n$ in disjoint translates of boxes $B_k$, for a given $k$ such that ${\Lambda }_n\subset [{\Lambda }_n]:=\cup D_k$

We need to show that in the limit the difference of the pressure goes to zero, i.e. we want to exstimate:

$$|{\psi }_{{\Lambda }_n}-\psi |\le |{\psi }_{{\Lambda }_n}-{\psi }_{[{\Lambda }_n]}|+|{\psi }_{[{\Lambda }_n]}-{\psi }_{B_k}|+|{\psi }_{B_k}-\psi |$$

Given ant $ϵ>0$, for any $k\ge k_1$ we now that the last term is less than $ϵ$ since ${\psi }_{B_k}\to \psi$.

Let’s compute ${\mathcal{H}}_{[{\Lambda }_n]}$:

$${\mathcal{H}}_{[{\Lambda }_n]}=\sum _j{\mathcal{H}}_{B_k^{(j)}}+W_n$$

Where the term $W_n$ is the energy due to the interaction between the regions $B_k$. The interaction can be bounded by

$$|W_n|\le 2d\beta \frac{|[{\Lambda }_n]|}{|B_k|}(2k+1{)}^{d-1}=2d\beta |[{\Lambda }_n]|(2k+1{)}^{-1}$$

so that

$$\frac{|[{\Lambda }_n]|}{|B_k|}{\mathcal{H}}_{B_k}-2d\beta |[{\Lambda }_n]|(2k+1{)}^{-1}\le {\mathcal{H}}_{[{\Lambda }_n]}\le \frac{|[{\Lambda }_n]|}{|B_k|}{\mathcal{H}}_{B_k}+2d\beta |[{\Lambda }_n]|(2k+1{)}^{-1}$$ $$\left|{\mathcal{H}}_{[{\Lambda }_n]}-\frac{|[{\Lambda }_n]|}{|B_k|}{\mathcal{H}}_{B_k}\right|\le 2d\beta |[{\Lambda }_n]|(2k+1{)}^{-1}$$

from this follows that the partition function is bounded by

$$e^{-2d\beta |[{\Lambda }_n]|(2k+1{)}^{-1}}{Z}_{B_k}^{\frac{|[{\Lambda }_n]|}{|B_k|}}\le Z_{[{\Lambda }_n]}\le e^{+2d\beta |[{\Lambda }_n]|(2k+1{)}^{-1}}{Z}_{B_k}^{\frac{|[{\Lambda }_n]|}{|B_k|}}$$

so that the pressure

$$|{\psi }_{[{\Lambda }_n]}-{\psi }_{B_k}|\le 2d\beta (2k+1{)}^{-1}<ϵ$$

for $k$ big enough, say $\forall k\ge k_2$.

Let us write ${\Delta }_n:=[{\Lambda }_n]\setminus {\Lambda }_n$, then it’s easy to see that

$$|{\mathcal{H}}_{[{\Lambda }_n]}(\omega )-{\mathcal{H}}_{{\Lambda }_n}(\omega {|}_{{\Lambda }_n})|\le (2d\beta +|h|)|{\Delta }_n|$$

so that for the partition function

$$Z_{[{\Lambda }_n]}=\sum _{\omega \in {\Omega }_{[{\Lambda }_n]}}{e}^{-{\mathcal{H}}_{[{\Lambda }_n]}(\omega )}\le \sum _{\omega \in {\Omega }_{[{\Lambda }_n]}}{e}^{-{\mathcal{H}}_{{\Lambda }_n}(\omega {|}_{\Lambda })+(2d\beta +|h|)|{\Delta }_n|}$$ $$=2^{|{\Delta }_n|}{Z}_{{\Lambda }_n}{e}^{(2d\beta +|h|)|{\Delta }_n|}$$

the same can be down for a lower bound. This yields

$$|\log Z_{{\Lambda }_n}-\log Z_{[{\Lambda }_n]}|\le (2d\beta +|h|)|{\Delta }_n|$$

we now use the Van Hove condition, since we can bound the number of spins in ${\Delta }_n$ by

$$|{\Delta }_n|\le |B_k||{\partial }^{in}{\Lambda }_n|$$

from this

$$\left|{\psi }_{{\Lambda }_n}-\frac{1}{|{\Lambda }_n|}\log Z_{[{\Lambda }_n]}\right|\le (2d\beta +|h|)|B_k|\frac{|{\partial }^{in}{\Lambda }_n|}{|{\Lambda }_n|}$$

for $n$ big enough, the right side is smaller than $ϵ$. Also the term inside the absolute values approches the pressure ${\psi }_{[{\Lambda }_n]}$ since

$$1\le \frac{|[{\Lambda }_n]|}{|{\Lambda }_n|}=1+\frac{|{\Delta }_n|}{|{\Lambda }_n|}\le 1+|B_k|\frac{|{\partial }^{in}{\Lambda }_n|}{|{\Lambda }_n|}\to 1$$

4. **Indipendence of boundary condition

This follows from the fact that

$$|{\mathcal{H}}_{\Lambda }^{\eta }(\omega )-{\mathcal{H}}_{\Lambda }(\omega )|\le (2d\beta +|h|)|{\partial }^{in}\Lambda |$$

so the finite volume pressures differ by a $O(|{\partial }^{in}\Lambda |/|\Lambda |$) which vanishes in the termodinamic limit thanks to the Van Hove condition. $\square$

Magnetization §

A natural macroscopic variable is the average magnetic moment, or the magnetization density:

$$m_{\Lambda }:=\frac{1}{|\Lambda |}\sum _{i\in \Lambda }{\sigma }_i$$

By direct computation

$$m_{\Lambda }^{\#}(\beta ,h)=\frac{\partial {\psi }_{\Lambda }^{\#}(\beta ,h)}{\partial h}$$

An interesting question is wether it holds in thermodynamic limit

$$m(\beta ,h)=\underset{{\Lambda }_n\uparrow {\mathbb{Z}}^d}{\lim }\frac{\partial {\psi }_{\Lambda }^{\#}(\beta ,h)}{\partial h}\stackrel{?}{=}\frac{\partial }{\partial h}\underset{{\Lambda }_n\uparrow {\mathbb{Z}}^d}{\lim }{\psi }_{\Lambda }^{\#}(\beta ,h)=\frac{\partial \psi (\beta ,h)}{\partial h}$$

This depends on the differentiability of $\psi$ w.r.t $h$. Since it’s convex, we know that the left and right derivatives always exists, and that $\psi$ is not differentiable in a set of measure zero.

Moreover, when $\psi$ is differentiable the limit exchange holds. This fact, that the magnetization density is discontinuous when $\psi$ is non differentiable, leads us to a first definition of phase transition:

Def (First order phase transition) The pressure $\psi$ exhibits a first order phase transition at $(\beta ,h)$ is it fails to be differentiable w.r.t $h$ in this point.

Nota that since $\psi$ in indipendent from the boudary conditions, if $\psi (h,\beta )$ is differentiable, the magnetization density in indipendent from the boundary condition, e.s. $+$ or $-$. This means that we don’t see a macroscopic instability. On the other hand, if $\psi$ fails to be differentiable, (hence we have a first order phase transition), the value of $m={\lim }_{n\to \infty }{m}_{{\Lambda }_n}^{\#}$ depends on the boundary conditions: we have sensibility form b.c.: macroscopic instability.

One-Dimensional Ising Model §

The 1D Ising model is exactly solvable, we can compute the pressure. This was Ising doctorate thesis main result. The trick is to a trasnfer matrix, and writing the partition function as the trace of power of this matrix.

For simplicity consider the periodic b.c. (we know that the pressure is insensitive to b.c.)

$$Z_{{\Lambda }_n,\beta ,h}=\sum _{\omega \in {\Omega }_{\Lambda }}{e}^{-{\mathcal{H}}_{{\Lambda }_n,\beta ,h}(\omega )}$$ $$\sum _{{\omega }_0=\pm 1}\sum _{{\omega }_1=\pm 1}\cdots \prod _{i=0}^{n-1}{e}^{\beta {\omega }_i{\omega }_{i+1}+h{\omega }_i}$$

We can define a $2\times 2$ matrix $A$

$$A=\left(\begin{array}{cc}{e}^{\beta +h}& e^{-\beta +h}\\ e^{-\beta -h}& e^{\beta -h}\end{array}\right)$$

if we compute $A^2$

$$A^2=\left(\begin{array}{cc}{e}^{\beta +h}{e}^{\beta +h}+e^{-\beta +h}{e}^{-\beta -h}& e^{\beta +h}{e}^{-\beta +h}+e^{-\beta +h}{e}^{\beta -h}\\ e^{-\beta -h}{e}^{\beta +h}+e^{\beta -h}{e}^{}& e^{-\beta -h}{e}^{-\beta +h}+e^{\beta -h}{e}^{\beta -h}\end{array}\right)$$

The trace is precisely $Z$ with two particles. In general

$$Z=Tr(A^N)={\lambda }_1^N+{\lambda }_2^N$$

thus the pressure is (since $|{\Lambda }_n|=N$)

$$\psi (\beta ,h)=\underset{n\to \infty }{\lim }\frac{1}{|{\Lambda }_n|}\log Z=\underset{N\to \infty }{\lim }\frac{1}{N}\log {\lambda }_1^N\left(1+\frac{{\lambda }_2^N}{{\lambda }_1^N}\right)=\log {\lambda }_1$$

where ${\lambda }_1$ is the maximum modulus eigenvalue so that

$${\left(\frac{{\lambda }_2}{{\lambda }_1}\right)}^N\to 0$$

the eigenvalues of $A$ are:

$${\lambda }_{1,2}=e^{\beta \cosh (h)}\pm \sqrt{e^{2\beta }{\cosh }^2(h)-2\sinh (2\beta )}$$

this shows that the pressure is analytic and differentiables for every value $(\beta ,h)$. We can conclude that there isn’t a first order phase transition.

One can compute the magnetization $m$ and show that it’s continuous, in particular the spontaneus magnetization

$$m^{\ast }(\beta ):=\underset{h\downarrow 0}{\lim }m(\beta ,h)=m(\beta ,0)=0\forall \beta \ge 0$$

Infinite volume Gibbs state §

Here we define an infinite volume Gibbs state, as a linear functional on local functions. The link of this section with Infinite-volume Gibbs measures is given by the Riesz representation theorem.

Def An Infinite-volume Gibbs state is a functional mapping a local function $f$ to a real number $⟨f⟩$ satisfying:

1. Normalization $⟨1⟩=1$
2. Positivity $⟨f⟩\ge 0$ when $f\ge 0$
3. linearity $⟨f+\alpha g⟩=⟨f⟩+\alpha ⟨g⟩$ for all $\alpha \in \mathbb{R}$ The number $⟨f⟩$ is called the average of $f$ in the state $⟨\cdot ⟩$.

It’s natural to define convergence of finite volume Gibbs distribution to infinite volume state, if for any local function $f$

$${\mu }_{{\Lambda }_n,\beta ,h}^{{\#}_n}(f)\to ⟨f⟩$$

This is precisley the notion of weak convergence of probability measure, where the average of $f$ as

$$⟨f⟩=\int fd\mu$$

Can we construct infinite volume Gibbs state as a limit of finite volume Gibbs distribution, in the sense of the previous limit? We study the case of two simple boundary conditions, which will be central in the analysis of the general case.

Theorem Let $\beta \ge 0$ and $h\in \mathbb{R}$. Given any sequence ${\Lambda }_n\uparrow {\mathbb{Z}}^d$, the finite volume Gibbs distribution with $+$ or $-$ boundary conditions converge to infinite volume Gibbs state:

$$⟨\cdot {⟩}_{\beta ,h}^{+}=\underset{n\to \infty }{\lim }⟨\cdot {⟩}_{{\Lambda }_n,\beta ,h}^{+}⟨\cdot {⟩}_{\beta ,h}^{-}=\underset{n\to \infty }{\lim }⟨\cdot {⟩}_{{\Lambda }_n,\beta ,h}^{-}$$

and the state obtained do not depend on the sequence ${\Lambda }_n$ and are both translation invariant.

Remark Not that in general $⟨\cdot {⟩}_{\beta ,h}^{+}\ne ⟨\cdot {⟩}_{\beta ,h}^{-}$. This is the case when at $(\beta ,h)$ there is a first order phase transition.

Proof We use a representation of a local function as sums of occupation numbers

$$f(\omega )=\sum _{A\subset supp(f)}{\hat{f}}_A{n}_A(\omega )$$

then by linearity the result is valid for all local functions, if we prove it for $n_A$ functions. Since $n_A$ are non-decreasing, we can use a consequence of the FKG inequality:

$$⟨n_A{⟩}_{{\Lambda }_n}^{+}\ge ⟨n_A{⟩}_{{\Lambda }_{n+1}}^{+}$$

thus this sequence is non-increasing, and since it’s non-negative it converges. Thus by linearity for each local function

$$\underset{n\to \infty }{\lim }⟨f{⟩}_{{\Lambda }_n}^{+}=⟨f{⟩}^{+}$$

is well defined. It’ linear, positive and normalized, so it’s a Gibbs state. To show volume sequence independence, let ${\Lambda }_n^1,{\Lambda }_n^2\uparrow {\mathbb{Z}}^d$ we build a new sequence ${\Delta }_k\uparrow {\mathbb{Z}}^d$ in the following way:

$${\Delta }_{2k-1}=\text{ some }{\Lambda }_n^1{\Delta }_{2k}=\text{ some }{\Lambda }_n^2\text{ s.t.}{\Delta }_{2k-1}\subset {\Delta }_{2k}$$

in words: we choose for odd numbers a set in ${\Lambda }^2$ and for even numbers a set in ${\Lambda }^2$, such that the sequence in increasing (we can always do that). Now the limit

$$⟨f{⟩}_{{\Delta }_k}^{+}\to ⟨f{⟩}^{+}$$

exists, but by construct ${\Delta }_k$ is a subsequence of both ${\Lambda }_1$ and ${\Lambda }_2$ hence their limit is the same.

Translation invariance follows from this, since we can cancel the effect of a translation of states by the inverse translation on the volumes, but we have just shown that the limit is indipendent from the sequence of volumes!

$$\underset{n\to \infty }{\lim }⟨f\circ {\theta }_i{⟩}_{{\Lambda }_n}^{+}=\underset{n\to \infty }{\lim }⟨f\circ {\theta }_i{⟩}_{{\theta }_{-i}{\Lambda }_n}^{+}=\underset{n\to \infty }{\lim }⟨f{⟩}_{{\Lambda }_n}^{+}=⟨f{⟩}^{+}\square$$

Criteria for uniqueness §

States prepared with $+$ and $-$ boundary conditions are usefull to study the question of uniquess of Gibbs states.

Theorem let $(\beta ,h)\in {\mathbb{R}}_{\ge 0}\times \mathbb{R}$. The following are equivalent:

1. There is a unique Gibbs state at $(\beta ,h)$
2. $⟨\cdot {⟩}_{\beta ,h}^{-}=⟨\cdot {⟩}_{\beta ,h}^{+}$
3. $⟨{\sigma }_0{⟩}_{\beta ,h}^{-}=⟨{\sigma }_0{⟩}_{\beta ,h}^{+}$

Proof $1⟹2⟹3$ are trivial. $2⟹1$ follows from the inequality we have proven:

$$⟨n_A{⟩}^{-}\le ⟨n_A⟩\le ⟨n_A{⟩}^{+}$$

but any local function can be written as linear combination of $n_A$. $3⟹2$ The function ${\sum }_{i\in A}{n}_i-n_A$ is non-decreasing, so that

$$⟨\sum _{i\in A}{n}_i-n_A{⟩}^{-}\le ⟨\sum _{i\in A}{n}_i-n_A{⟩}^{+}$$

using linearity and rearrenging

$$\sum _{i\in A}(⟨n_i{⟩}^{+}+⟨n_i{⟩}^{-})\ge ⟨n_A{⟩}^{+}-⟨n_A{⟩}^{-}$$

but in the limit, using translation invariance the left hand side vanishes. So for any local function $f$ the averages coincide. $\square$

Correlation inequalities §

Theorem (GKS inequality) Let $j_{ij}$ and $h_i$ be collections of non-negative real numbers. Then, for all $A,B\subset \Lambda$,

$$⟨{\sigma }_A{⟩}_{\Lambda ,J,h}^{+}\ge 0⟨{\sigma }_A{\sigma }_B{⟩}_{\Lambda ,J,h}^{+}\ge ⟨{\sigma }_A{⟩}_{\Lambda ,J,h}^{+}⟨{\sigma }_B{⟩}_{\Lambda ,J,h}^{+}$$

Theorem (FKG inequality) Let $f$ and $g$ be non-decreasing function, $J_{ij}$ be a collection of non-negative real numbers, $h$ a collection of real numbers (we allow negative values), $\#$ any boundary condition, then

$$⟨fg{⟩}_{\Lambda ,J,h}^{\#}\ge ⟨f{⟩}_{\Lambda ,J,h}^{\#}⟨g{⟩}_{\Lambda ,J,h}^{\#}$$

From FKG inequality follows an intuitive inequality if we consider non-decreasing function $f$ and two volumes ${\Lambda }_1\subset {\Lambda }_2$:

$$⟨f{⟩}_{{\Lambda }_1,\beta ,h}^{+}\ge ⟨f{⟩}_{{\Lambda }_2,\beta ,h}^{+}$$

since the indicator function $1({\sigma }_i=1\forall i\in {\Lambda }_2\setminus {\Lambda }_1)$ is non-decreasing.

$$⟨f{⟩}_{{\Lambda }_1,\beta ,h}^{+}=\frac{⟨f1({\sigma }_i=1\forall i\in {\Lambda }_2\setminus {\Lambda }_1){⟩}_{{\Lambda }_2,\beta ,h}^{+}}{⟨1({\sigma }_i=1\forall i\in {\Lambda }_2\setminus {\Lambda }_1){⟩}_{{\Lambda }_2,\beta ,h}}\ge ⟨f{⟩}_{{\Lambda }_2,\beta ,h}^{+}$$

Non-decreasing functions are functions that “like” $+1$ spins. In this sense it’s intuitive to think of the boudnary conditions $-$ and $+$ as extremal.

Lemma Let $f$ be a non-decreasing function. Then for any boundary condition $\eta$, and $\beta \ge 0$, $h\in \mathbb{R}$, $\Lambda ⋐{\mathbb{Z}}^d$

$$⟨f{⟩}_{\Lambda ,\beta ,h}^{-}\le ⟨f{⟩}_{\Lambda ,\beta ,h}^{\eta }\le ⟨f{⟩}_{\Lambda ,\beta ,h}^{+}$$

Proof Let $I(\omega ):=e^{\beta {\sum }_{i\sim ji\in \Lambda ,j\notin \Lambda }{\omega }_i(1-{\eta }_j)}$ and note that

$$\sum _{\omega \in {\Omega }_{\Lambda }^{+}}{e}^{-\mathcal{H}(\omega )}=\sum _{\omega \in {\Omega }_{\Lambda }^{\eta }}{e}^{-\mathcal{H}(\omega )}I(\omega )$$ $$\sum _{i\sim ji,j\in \Lambda }{\omega }_i{\omega }_j+\sum _{i\sim ji\in \Lambda ,j\notin \Lambda }{\omega }_i{\omega }_j+\sum _{i\sim ji\in \Lambda ,j\notin \Lambda }{\omega }_i(1-{\eta }_j)$$

but $j\notin \Lambda$ so ${\omega }_j={\eta }_j$.

$$\sum _{i\sim ji\in \Lambda ,j\notin \Lambda }{\omega }_{i}1$$

these are the $+$ boundary conditions. Then

$$\sum _{\omega \in {\Omega }_{\Lambda }^{+}}{e}^{-\mathcal{H}(\omega )}f(\omega )\ge \sum _{\omega \in {\Omega }_{\Lambda }^{\eta }}{e}^{-\mathcal{H}(\omega )}I(\omega )f(\omega )$$

using FKG inequality, since $I$ is non-decreasing also

$$⟨f{⟩}_{\Lambda }^{+}\ge \frac{{\sum }_{\omega \in {\Omega }_{\Lambda }^{+}}{e}^{-\mathcal{H}(\omega )}f(\omega )}{{\sum }_{\omega \in {\Omega }_{\Lambda }^{+}}{e}^{-\mathcal{H}(\omega )}}\ge \frac{{\sum }_{\omega \in {\Omega }_{\Lambda }^{\eta }}{e}^{-\mathcal{H}(\omega )}I(\omega )f(\omega )}{{\sum }_{\omega \in {\Omega }_{\Lambda }^{\eta }}{e}^{-\mathcal{H}(\omega )}I(\omega )}=\frac{⟨fI{⟩}_{\Lambda }^{\eta }}{⟨I{⟩}_{\Lambda }^{\eta }}\ge ⟨f{⟩}_{\Lambda }^{\eta }$$

Spontaneus symmetry breaking at low temperatures §

Characterization of uniqueness so far:

$$\frac{\partial \psi (\beta ,h)}{\partial h}\text{ exists }⟺m^{-}(\beta ,h)=m^{+}(\beta ,h)⟺⟨{\sigma }_0{⟩}_{\beta ,h}^{-}=⟨{\sigma }_0{⟩}_{\beta ,h}^{+}$$

Our goal is to prove that ${\beta }_c(d)<\infty$ for all $d\ge 2$. To do so it’s sufficient to show that

$${\mu }_{\Lambda ,\beta ,0}^{+}({\sigma }_0=-1)\le \delta (\beta )$$

where $\delta (\beta )\to 0$ when $\beta \to \infty$.

This follows form

$$⟨{\sigma }_0{⟩}_{\Lambda ,\beta ,0}^{+}={\mu }_{\Lambda ,\beta ,0}^{+}({\sigma }_0=+1)-{\mu }_{\Lambda ,\beta ,0}^{+}({\sigma }_0=-1)$$ $$=1-2{\mu }_{\Lambda ,\beta ,0}^{+}({\sigma }_0=-1)$$

so that for $\beta$ large enough $⟨{\sigma }_0{⟩}_{\Lambda ,\beta ,0}^{+}>0$ but this implies, since we have symmetry by spin reverse ($h=0$)

$$⟨{\sigma }_0{⟩}_{\Lambda ,\beta ,0}^{-}=-⟨{\sigma }_0{⟩}_{\Lambda ,\beta ,0}^{+}$$

so we can conclude that

$$⟨{\sigma }_0{⟩}_{\Lambda ,\beta ,0}^{-}\ne ⟨{\sigma }_0{⟩}_{\Lambda ,\beta ,0}^{+}$$

since

$$m^{\ast }(\beta ):=\underset{h\downarrow 0}{\lim }m(\beta ,h)=\underset{h\downarrow 0}{\lim }{m}^{+}(\beta ,h)=m^{+}(\beta ,0)=⟨{\sigma }_0{⟩}_{\beta ,0}^{+}$$

we define the critical temperature as

$${\beta }_c(d):=\inf \{\beta \ge 0:m^{\ast }(\beta )>0\}$$

Peierls’ argument §

First a simple revrite of the Hamiltonian

$${\mathcal{H}}_{\Lambda ,\beta ,0}=-\beta \sum _{(i,j)\in E_{\Lambda }}{\sigma }_i{\sigma }_j=-\beta |E_{\Lambda }|+\beta \sum _{(i,j)\in E_{\Lambda }}(1-{\sigma }_i{\sigma }_j)$$

Dual lattice ${\mathbb{Z}}_{\ast }^d:={\mathbb{Z}}^d+(\frac{1}{2},\frac{1}{2})$ We are surronding each spin $i$ with a unit squared $Q_i$ centered at the spin. Our goal is to build “island” of negative spins (in a sea of positive ones):

$$M(\omega ):=\bigcup _{i\in \Lambda :{\sigma }_i=-1}{Q}_i$$

the the boundary of this set $\partial M(\omega )$ is composed of edges in the dual lattice: each edge separates two opposite sign spins, thus we can rewrite the Hamiltonian as

$$-\beta |E_{\Lambda }|+2\beta |\partial M(\omega )|$$

we now decompose $\partial M(\omega )$ in disjoint sets (islands), by introducing a deformation rule to take care of possibile intersection of the form $+$. Now $\partial M$ is a union of closed curves

$$\partial M(\omega )={\gamma }_i\cup {\gamma }_2\cup \cdots \cup {\gamma }_n$$

each curve is called a contour path of $\omega$, we denote their lenght with $|\gamma |$. We again rewrite the hamiltonian as

$$-\beta |E_{\Lambda }|+2\beta \sum _{\gamma \in \Gamma (\omega )}|\gamma |$$

thus the partition function is

$$Z_{\Lambda ,\beta ,0}^{+}=\sum _{\omega \in {\Omega }_{\Lambda }^{+}}{e}^{\beta |E_{\Lambda }|-2\beta {\sum }_{\gamma \in \Gamma (\omega )}|\gamma |}$$

the constant term $\beta |E_{\Lambda }|$ doesn’t change probabilities, since it cancels out:

$$\mu (\omega {)}_{\lambda ,\beta ,0}^{+}=\frac{e^{-2\beta {\sum }_{\gamma \in \Gamma (\omega )}|\gamma |}}{{\sum }_{\omega \in {\Omega }_{\Lambda }^{+}}{e}^{-2\beta {\sum }_{\gamma \in \Gamma (\omega )}|\gamma |}}$$

Notice that if ${\sigma }_0=-1$, then there exists a contour curve $\gamma$ such that $0\in Int(\gamma )$. We can bound the probability:

$$\mu ({\sigma }_0=-1{)}_{B(n),\beta ,0}^{+}\le \mu (\exists \gamma :0\in Int(\gamma ){)}_{B(n),\beta ,0}^{+}$$ $$\le \sum _{\gamma :Int(\gamma )\ni 0}\mu (\gamma \in \Gamma {)}_{B(n),\beta ,0}^{+}$$

Claim For all $\beta >0$ and any contour $\gamma$:

$$\mu (\gamma \in \Gamma {)}_{B(n),\beta ,0}^{+}\le e^{-2\beta |\gamma |}$$

Proof

$$\mu (\gamma \in \Gamma {)}_{B(n),\beta ,0}^{+}=\sum _{\omega :\gamma \in \Gamma (\omega )}\mu (\omega {)}_{B(n),\beta ,0}^{+}$$ $$=e^{-2\beta |\gamma |}\frac{{\sum }_{\omega :\gamma \in \Gamma (\omega )}{\prod }_{\Gamma \setminus \gamma }{e}^{-2\beta |{\gamma }^{\prime }|}}{{\sum }_{\omega \in {\Omega }_{\Lambda }^{+}}{\prod }_{\Gamma }{e}^{-2\beta |{\gamma }^{\prime }|}}$$

we need to show that the big fraction is bounded above by $1$. Indeed the sum in the denominator is the same as the denominator, with an additional constraint. Indeed a given configuration such that $\Gamma (\omega )\ni \gamma$, can be transformed into one that doesn’t contain $\gamma$, simply by flipping all the spins inside $Int(\gamma )$. The new state has contour sets precisley $\Gamma (\omega )\setminus \{\gamma \}$ Call $C(\gamma )$ the set of configurations that can be obtained by removing $\gamma$, clearly $C(\gamma )\subseteq {\Omega }_{B(n)}^{+}$ so that

$$\sum _{\omega :\gamma \in \Gamma (\omega )}\prod _{\Gamma \setminus \gamma }{e}^{-2\beta |{\gamma }^{\prime }|}=\sum _{{\omega }^{\prime }\in C(\gamma )}\prod _{{\gamma }^{\prime }\in \Gamma }{e}^{-2\beta |{\gamma }^{\prime }|}$$

We have reached

$$\mu ({\sigma }_0=-1{)}_{B(n),\beta ,0}^{+}\le \sum _{\gamma :0\in Int(\gamma )}{e}^{-2\beta |\gamma |}$$

we now divide these curves that enclose the origin by thei lenght, and asking how many exists of a fixed length. Clearly the shorter one has length $4$.

$$\mu ({\sigma }_0=-1{)}_{B(n),\beta ,0}^{+}\le \sum _{k\ge 4}{e}^{-2\beta k}\#\{\gamma :0\in Int(\gamma )|\gamma |=k\}$$

we can easly bound the number of contour paths of fixed lenght: at the first step i have $4$ choices, the only $3$ (we cant go back) so the number of paths of length $k$ is $4\cdot 3^{k-1}$. For every curve we can assign a given spin it crosses, since the most a contour of length $k$ can travel is $\lfloor \frac{k}{2}\rfloor$ there are at most $k^2$ curves that contain the origin. In the end

$$\mu ({\sigma }_0=-1{)}_{B(n),\beta ,0}^{+}\le \frac{4}{3}\sum _{k\ge 4}{k}^2{3}^k{e}^{-2\beta k}=:\delta (\beta )$$

which converges if $2\log k/k+\log 3-2\beta <1$ and goes to zero when $\beta \to \infty$. This proves that ${\beta }_c(2)<\infty$.