Recurrent McCulloch-Pitts network dynamics

Dinamica §

Possiamo introdurre una dinamica discreta tra stati di una rete di McCulloch-Pitts neuron $S(t)$:

$$S_i(t+\Delta t)=\Theta \left(\sum _{j=1}^N{J}_{ij}{S}_j(t)+U_i^{\ast }\right)$$

Si può pensare a $\Delta t$ come un tempo refrattario dei neuroni biologici.

Ci sono due maniera di realizzare questa dinamica:

• Dinamica parallela Gli stati evolvono tutti insiemi;
• Dinamica sequenziale Si sceglie un neurone $i$ e si aggiorna solo quello.

Noiseless recurrent networks §

Studiamo la dinamica nel caso $T=0$ noiseless per i casi

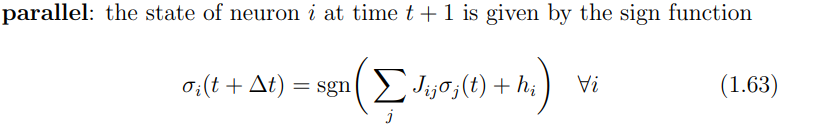
Parallel dynamics §

Es 1 Caso banale: $J_{ij}=0$ e $h_i\ne 0$. La regola di update è banale, non dipende dallo stato precedente, dopo una iterazione tutto il sistema va nello stato finale:

$${\sigma }_i=sign(h_i)$$

Il bacino di attrazione per questo stato punto fisso è tutto il dominio $\mathcal{D}=\{-1,1{\}}^N$. Es 2 Supponiamo ora $J_{ij}=\frac{J}{N}$ e $h_i=0$, ovvero interazioni simmetriche e campo esterno nullo. Otteniamo la regola di update: 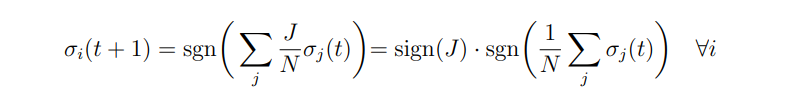Notiamo come compare un’osservabile macroscopica, la magnetizzazzione media (spin medio):

$$m(t):=\frac{1}{N}\sum _{i=1}^N{\sigma }_i(t)$$

Possiamo ottenere una formula di update per questa osservabile macroscopica sommando:

$$m(t+1)=\frac{1}{N}\sum _{i=1}^N{\sigma }_i(t+1)=\frac{sign(J)}{N}\sum _{i=1}^{N}sign(m(t))=sign(J)\cdot sign(m(t))$$

Se $J>0$, abbiamo una dinamica imitatoria: i neuroni tendono a fare quello che fanno gli altri. Partizioniamo le configurazioni in:

$${\mathcal{D}}^{+}:=\{\sigma \in \{-1,1{\}}^N:m(\sigma )>0\}{\mathcal{D}}^{-}:=\{\sigma \in \{-1,1{\}}^N:m(\sigma )<0\}$$

(supponiamo di avere un numero dispari di neuroni, così non abbiamo il caso patologico $m=0$).

Abbiamo punti fissi $\{-1,-1,\dots {\}}^N$ e $\{+1,\dots ,+1{\}}^N$ che corrispondono a $m=-1$ e $m=1$.

Se $J<0$ abbiamo un ciclo limite di periodo due tra stati $m=1$ ed $m=-1$.

Es 3 Caso $J_{ij}=\frac{J}{N}$ e $h_i=h\ne 0$. La regola di update della magnetizzazzione media è:

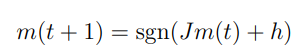
Se il campo esterno $h$ è troppo forte, ovvero $|h|>|J|$ otteniamo una dinamica banale, come nel caso senza interazioni.

Con $J>0$ otteniamo sempre due punti fissi, ma con bacini d’attrazione non uguali e che dipendono dal rapporto $\frac{h}{J}$.

Con $J<0$ otteniamo sempre un ciclo di periodo due, $\frac{h}{J}$ controlla quanto ci metto a raggiungere il ciclo.

Sequential dynamics §

Studiamo gli stati limite tramite Funzioni di Lyapunov.

Proposizione Se abbiamo interazioni simmetriche $J_{ij}=J_{ji}$, ed autointerazioni non negative $J_{ii}\ge 0$, un campo esterno $h_i$ e noisless ($T=0$), allora

$$L(\sigma ):=-\frac{1}{2}\sum _{i,j}{J}_{ij}{\sigma }_i{\sigma }_J-\sum _i{h}_i{\sigma }_i$$

è una funzione di Lyapunov della dinamica sequenziale:

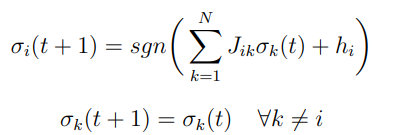
dove si estrae $i$ uniformemente in $[1,N]$.

Durante la dinamica la funzione evolve:

$$\Delta L=L(\sigma (t+1))-L(\sigma (t))=-2\left|\sum _{j=1}^N{J}_{ij}{\sigma }_j+h_i\right|-2J_{ii}\le 0$$

Siccome $L(\sigma )$ è limitata inferiormente, ammette un minimo ed il sistema arriverà a queste configurazioni e si fermerà. (Richiediamo distanza di hamming $1$).

Pattern retrival §

Possiamo vedere questa abilità delle reti di “ricordare” informazioni $\sigma (\infty )$, dato un input iniziale $\sigma (0)$, sfruttando questa dinamica verso attrattori.

Basando sulla regola (principio) di Hebb:

Neurons that fire together wire together Neurons out of sync fail to link

Risulta ragionevole: 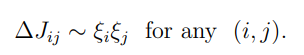Si vede facilmente che possiamo memorizzare singoli pattern $\xi$ definendo le connessioni in accordo con la regola di Hebb. Aggiungere campo esterno complica le cose, valgono le stesse considerazioni fatte nella dinamica parallela caso $J$ simmetrico con campo esterno. Quindi la rete avrà punti fissi in $\xi$ e $-\xi$, a seconda di $\frac{h}{J}$.

Per più pattern, una scelta ragionevole è mediare: 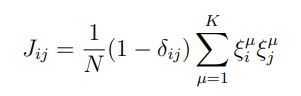Per semplificare la trattazzione assumiamo che i pattern siano ortogonali.

Proposizione La dinamica sequenziale applicata ad una rete con pesi dati dalla regola di Hebb e $h_1=0$, mostra $2K$ stati stazionari, che corrispondono ai pattern ed hai loro inversi.

Dim Scriviamo la funzione di Lyapunov:

$$L(\sigma )=-\frac{1}{2}\sum _{ij}{J}_{ij}{\sigma }_i{\sigma }_j+-\sum _i{\sigma }_i{h}_i$$

con la regola di Hebb e campi esterni nulli

$$=\frac{1}{2N}\sum _{ij}({\delta }_{ij}-1)\left[\sum _{\mu =1}^K{\xi }_i^{\mu }{\xi }_j^{\mu }\right]{\sigma }_i{\sigma }_j$$ $$=\frac{1}{2N}\sum _{ij}\left[\sum _{\mu =1}^K{\xi }_i^{\mu }{\xi }_j^{\mu }\right]{\sigma }_i{\sigma }_j+\frac{1}{2}K$$

notando che

$${\left(\sum _{i=1}^N{\xi }_i^{\mu }{\sigma }_i\right)}^2=\sum _{ij}{\xi }_i^{\mu }{\xi }_j^{\mu }{\sigma }_i{\sigma }_j$$

dunque

$$L(\sigma )=-\frac{1}{2}\sum _{\mu =1}^K{\left(\frac{1}{\sqrt{N}}\sum _{i=1}^N{\xi }_i^{\mu }{\sigma }_i\right)}^2+\frac{1}{2}K$$

Il termine al quadrato non è altro che il prodotto scalare tra lo stato ed il pattern (normalizzato) ${\xi }_i$. Siccome abbiamo supposto per ipotesi che i pattern sono ortogonali, per massimizzare il prodotto scalare $\sigma$ deve avere la stessa direzione di $\xi$, ed in questo caso $⟨\xi ,\sigma ⟩=\pm \Vert \sigma \Vert$ e zero per gli altri pattern, dunque:

$$L(\sigma )\ge \frac{1}{2}K-\frac{1}{2}N$$

ed il minimo si ottiene quando $\sigma =\pm \xi$.

Osservazione Non è vero che tutti i minimi sono pattern, esistono dei minimi spuri.

$${\sigma }_i=sgn({\xi }_i^1+{\xi }_i^2+\dots )$$

Proposizione Misture dispari dei pattern sono stati stazionari. Misture pari sono stati stazionario instabili. Sono minimi locali.

Stocasticità §

Introduciamo delle perturbazioni random sulla soglia di attivazione, sommando una variabile a media nulla:

$$U_i^{\ast }(t)=U_i^{\ast }+\frac{1}{2}T{z}_i(t)$$

dove $\frac{1}{2}T$ è la deviazione standard, $z(t)$ una variabile a media nulla e varianza unitaria. Il parametro $T$ controlla dunque il grado di stocasticità (una temperatura).

Effettuiamo anche in cambio da $S_i=\{0,1\}$ a spin ${\sigma }_i=\{1,-1\}$. La regola di update diventa:

$${\sigma }_i(t+\Delta t)=sign\left[{\phi }_i(t)+T{z}_i(t)\right]{\phi }_i(t)=\sum _{j=1}^N{J}_{ij}{\sigma }_j(t)+h_i$$

da qui si capisce il fattore $1/2$ aggiunto al rumore. La quantità $\phi (t)$ viene detto campo locale.

La probabilità di trovare un neurone nello stato ${\sigma }_i=1,-1$ al tempo $t+\Delta t$ è dunque una variabile aleatoria che dipende dalle v.a. $z_i(t)$ e dallo stato della rete $\sigma (t)$. Se supponiamo sia simmetrico:

$$\mathbb{P}[{\sigma }_i(t+\Delta t)=1]=\mathbb{P}[{\phi }_i(t)>-T{z}_i(t)]={\int }_{{\phi }_i(t)/T}^{\infty }\mathbb{P}[z_i(t)=z]dz$$ $$\mathbb{P}[{\sigma }_i(t+\Delta t)=-1]=\mathbb{P}[{\phi }_i(t)<-T{z}_i(t)]={\int }_{-\infty }^{-{\phi }_i(t)/T}\mathbb{P}[z_i(t)=z]dz$$

esprimento il tutto in funzione della cumulativa $g(x)$

$$\mathbb{P}[{\sigma }_i(t+1)=\pm 1]=g(\pm {\phi }_i(t)/T)$$

Con $z_i(t)\sim N(0,1)$ la cumulativa è $erf(x)$; un’altra scelta simile è la tangente iperbolica:

$$g(x)=\frac{1}{2}\left(1+\tanh (x)\right)$$

a cui corrisponde un rumore distribuito come:

$$\mathbb{P}[z_i(t)=x]=\frac{1}{2}\left(1-{\tanh }^2(x)\right)$$

Per la dinamica parallela, supponendo le variabili indipendenti, la probabilità fattorizza e si ottiene:

$$\mathbb{P}(\sigma (t+1))=\prod _{i=1}^N\mathbb{P}({\sigma }_i(t+1)=\pm 1)=\prod _{i=1}^{N}g({\sigma }_i(t+1){\phi }_i(t)/T)$$

Noisy dynamics §

Vogliamo studiare il comportamento della rete quando aggiungiamo del rumore nelle soglie di attivazione, come abbiamo precedentemente mostrato. A causa del rumore random, potremmo solo fare considerazioni di carattere probabilistico sul comportamento della rete. Siamo sempre interessati al comportamento limite $\sigma (\infty )$. E’ chiaro che possiamo studiare lo stato limite tramite le catene di Markov. Sotto opportune ipotesi sulle interazioni, riusciamo a calcolare la distribuzione di equilibrio.

Matrice di transizione della dinamica sequenziale §

Abbiamo visto che una scelta sensata per la distribuzione del rumore, è quella con funzione di partizione

$$g(x)=\frac{1}{2}\left(1+\tanh (x)\right)\mathbb{P}[{\sigma }_i(t+1)=\pm 1]=g(\pm {\phi }_i(t)/T)$$

essendo molto simile al rumore gaussiano, senza l’impiccio della $erf(x)$. Vogliamo trovare la matrice di transizione $W$ di dimensione $2^N\times 2^N$. Se assumiamo di scegliere in maniera uniforme lo spin ${\sigma }_i$ da aggiornare, affinchè due pattern $\sigma$ e ${\sigma }^{\prime }$ abbiamo probabilità positiva devono essere necessariamente a distanza di Hamming uno:

$$W(\sigma ;{\sigma }^{\prime })=\frac{1}{N}\sum _{i=1}^N\left[\frac{1}{2}(1+{\sigma }_i\tanh \beta {\phi }_i({\sigma }^{\prime })){\delta }_{\sigma ,{\sigma }^{\prime }}+\frac{1}{2}(1-{\sigma }_i\tanh \beta {\phi }_i({\sigma }^{\prime })){\delta }_{F_i\sigma ,{\sigma }^{\prime }}\right]$$

dove il primo termine della sommatoria considera il caso in cui il pattern rimane lo stesso, il secondo nel caso in cui lo spin $i$ cambia segno. Con $F_i\sigma$ intendiamo lo stato ${\sigma }_j^{\prime }={\sigma }_j$ quando $j\ne i$ e ${\sigma }_i^{\prime }=-{\sigma }_i$.

Il processo di Markov associato a questa matrice di transizione è ergodico, ovvero indipendnetemente della distribuzione iniziale $p_0(\sigma )$ esiste un tempo finito $\tau$ tale che:

$$p_t(\sigma )>0\forall t\ge \tau$$

in maniera equivalente

$$W^t(\sigma ;{\sigma }^{\prime })>0\forall t\ge \tau$$

è chiaro che nel nostro caso sequenziale $\tau =N$.

Teorema Processi di Markov ergodici hanno un’unica distribuzione stazionario $p_{\infty }$ alla quale convergono indipendentemente dalla distribuzione iniziale.

$$p_{\infty }(\sigma )=\sum _{{\sigma }^{\prime }}W(\sigma ;{\sigma }^{\prime })p_{\infty }({\sigma }^{\prime })$$

Per calcolare esplicitamente la distribuzione stazionaria, aggiungiamo l’ipotesi di dettaglio bilanciato:

$$W(\sigma ;{\sigma }^{\prime })p_{\infty }({\sigma }^{\prime })=W({\sigma }^{\prime };\sigma )p_{\infty }(\sigma )\forall \sigma ,{\sigma }^{\prime }$$

Teorema La dinamica sequenziale senza autointerazioni, e con interazione simmetriche implica il dettaglio bilanciato. La distribuzione stazionaria di equilibrio è data da:

$$p_{\infty }(\sigma )\propto e^{-\beta \mathcal{H}(\sigma )}$$ $$\mathcal{H}(\sigma )=-\frac{1}{2}\sum _{ij}^N{J}_{ij}{\sigma }_i{\sigma }_j-\sum _{i=1}^N{h}_i{\sigma }_i$$

che è proprio la distribuzione di Boltzmann-Gibbs.

Remark L’hamiltoniana è proprio la funzione di Lyapunov del caso noisless, infatti nel limite $T\to 0$ la distribuzione stazionaria si picca intorno ai minimi di $\mathcal{H}$.

Proof* Siamo nelle ipotesi senza autointerazioni ed interazioni simmetriche:

$$J_{ii}=0J_{ij}=J_{ji}\forall ij$$

facciamo vedere che questo vale se e solo se vale il bilancio dettagliato

$$W(\sigma ;{\sigma }^{\prime })p_{\infty }({\sigma }^{\prime })=W({\sigma }^{\prime };\sigma )p_{\infty }(\sigma )\forall \sigma ,{\sigma }^{\prime }$$

Il caso $\sigma ={\sigma }^{\prime }$ è triviale. Resta il caso $F_i\sigma ={\sigma }^{\prime }$. La condizione di DB diventa

$$\frac{e^{-\beta F_i{\sigma }_i\phi (F_i\sigma )}}{\cosh \beta {\phi }_i(F_i\sigma )}{p}_{\infty }(F_i\sigma )=\frac{e^{-\beta {\sigma }_i\phi (\sigma )}}{\cosh \beta {\phi }_i(\sigma )}{p}_{\infty }(\sigma )$$

Siccome siamo nell’ipotesi di no autointerazioni i campi locali:

$${\phi }_i(F_i\sigma )={\phi }_i(\sigma )$$

sono indipendenti dal valore di ${\sigma }_i$!

Resta da far vedere che

$$e^{-\beta F_i{\sigma }_i{\phi }_i(F_i\sigma )}{p}_{\infty }(F_i\sigma )=e^{-\beta {\sigma }_i{\phi }_i(\sigma )}{p}_{\infty }(\sigma )$$

Sfruttiamo il fatto che $\forall \sigma$

$$p_{\infty }(\sigma )=\exp \beta \left(\sum _k{h}_k{\sigma }_k+\sum _{k\ne l}{J}_{kl}{\sigma }_k{\sigma }_l+K(\sigma )\right)$$

studiando all’esponente solo i termini che dipendono da ${\sigma }_i$

$$\frac{1}{2}\sum _{k\ne i}{\sigma }_i(J_{ki}-J_{ik}){\sigma }_k+K(\sigma )$$

DB vale se e solo se

$$K(F_i\sigma )-K(\sigma )={\sigma }_i\sum _{k\ne i}(J_{ki}-J_{ik}){\sigma }_k\forall \sigma ,i$$