Semigroup

in short: a group without the identity so that we don’t even need iverses.

Def (Semigroup) A set $S$ and a binary function $\gamma :S\times S\to S$ are called a semigroup if

1. $\forall s_1,s_2,s_3\in S$ $\gamma (s_1,\gamma (s_2,s_3))=\gamma (\gamma (s_1,s_2),s_3)$

A semigroup is an associative magma.

Notation: $\mathcal{S}=(S,\cdot )$ where we use the cleaner intrafix notation. It’s also common to call the semigroup with the same symbol as its support (universe) set.

There is a natural way to define a new semigroup starting from one, with support the power set of the orginial one.

We start with the semigroup $(S,\cdot )$. We claim that $(2^S,\circ )$ is a semigroup, when the operation between subsets is defines as

$$X\circ Y:=\{xy:x\in X,y\in Y\}$$

Clealry it’s closed, since we get another subset of $S$. It’s also associative, since: every element in $X\circ (Y\circ Z)$ can be written as $x(yz)=(xy)z$, this are precisley the elemetns in $(X\circ Y)\circ Z$.

Def (sub-semigroup) Starting from a semigroup $\mathcal{S}=(S,\cdot )$ given a subset $H\subseteq S$ we say that $\mathcal{H}=(H,\cdot {|}_{H\times H})$ is a semigroup of $\mathcal{S}$ and write $\mathcal{H}\le \mathcal{S}$ if it is closed w.r.t. $\cdot$.

Oss Associativity is eredited from $S$.

An interesting question is, given any subset $X\subseteq S$, find the smallest semigroup that contains $X$. This can be done as usuale for the Sigma algebra generated by a set.

Call $\{{\mathcal{T}}_{\gamma }{\}}_{\gamma \in \Gamma }$ the family of evert semigroup of $S$ that contain $X$ in their support. Then

$$⟨X⟩:=\bigcap _{\gamma \in \Gamma }{\mathcal{T}}_{\gamma }$$

is the smallest sub-semigropu of $S$ that contains $X$ in its support. Proof EZ. $\square$

Semigroup homomorphism §

As usual, the homomorphism is an operation beetween the support of algebraic structers that preserves their structure, i.e. it behaves well w.r.t. thei operation.

Let $\mathcal{S}=(S,\cdot )$ and $\mathcal{T}=(T,\ast )$ be two semigroups. A total mapping $\varphi :S\to T$ is called a semigroup morphism if $\forall s_1,s_2\in S$

$$\varphi (s_1\cdot s_2)=\varphi (s_1)\ast \varphi (s_2)$$

(the morphism property)

Birkhoff classification of morphism:

1. Epi-morphism: $\varphi$ is surjective
2. Mono-morphism: $\varphi$ is injective
3. Iso-morphism: $\varphi$ is bijective
4. Endo-morphism: $T\subseteq S$
5. Auto-morphism: $T=S$ and $\varphi$ bijective

Congruence of semigroups §

Let $R\subseteq S\times S$ be an equivalence realtion in $S$. We use the notation $xRy$ if $xy\in R$.

For all $s_1,s_2,t\in S$, $R$ is called a

right-conrguence of $S$ if: $s_{1}R{s}_2=(s_{1}t)R(s_{2}t)$ left-conrguence of $S$ if: $s_{1}R{s}_2=(t{s}_1)R(t{s}_2)$

congruence of $S$ if is both a left and a right-congruence.

We can define a new semigroup with the equivalance classes of $S$ under $R$.

Let $S/R:=\{[s{]}_R:s\in S\}$ the quotient set of $S$ under $R$. this will be our new support. We define the operation on the equivalence classes as: $\forall [s],[t]\in S/R$

$$[s]\circ [t]:=[s\cdot t]$$

Claim $(S/R,\circ )$ is a semigroup. Proof Clealry it’s close. Let’s prove associativity:

$$([s]\circ [t])\circ [r]=[s\cdot t]\circ [r]=[(s\cdot t)\cdot r]$$ $$=[s\cdot (t\cdot r)]=[s]\circ [t\cdot r]=[s]\circ ([t]\circ [r])$$

If $R$ is a congruence for the semigroup $S$, then the function that maps any element into its equivalence class, called the canonic morphism

$${\pi }_R:S\to S/R,s\mapsto [s]$$

is an epi-homorphism from ($S,\cdot )$ to $(S/R,\circ )$, since

$${\pi }_R(s_1\cdot s_2)=[s_1\cdot s_2]=[s_1]\circ [s_2]={\pi }_R[s_1]\circ {\pi }_R[s_2]\square$$

Given any morphism $\varphi :S\to T$, we can create a congruence on $S$, the canonic congruence of $\varphi$ $R_{\varphi }$. $\forall s_1,s_2\in S$

$$s_1{R}_{\varphi }{s}_2⟺\varphi (s_1)=\varphi (s_2)$$

Oss If $\varphi$ is a mono-morphism (injective) then $R_{\varphi }$ is trivial.

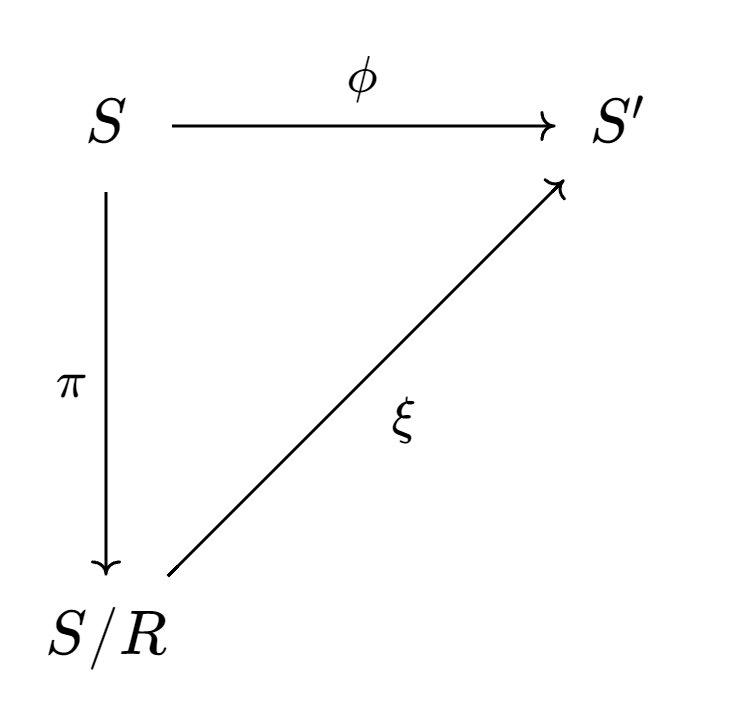
Theorem (fondamental theorem of semigroup morphism) Let $\varphi :S\to S^{\prime }$ be an epi-morphism (surjective), and let $R=R_{\varphi }$ be its canonic conrgruence relation and $\pi ={\pi }_R$ its canonic epi-morphism. Then there exists an isomorphism (bijective)

$$\xi :S/R\to S^{\prime }$$

such that

$$\varphi (s)=\xi (\pi (s))\forall s\in S$$

Which can be written also as $\varphi =\xi \circ \pi$.

This theorem can be written as the commutative diagram: