Legendre transform §

Suppose $L:{\mathbb{R}}^n\to \mathbb{R}$ is a function such that:

• is convex;
• ${\lim }_{|v|\to \infty }\frac{L(v)}{|v|}=+\infty$ (Note that convexity implies continuity).

Then we can define Def The Legendre transform of $L$ is the function

$$L^{\ast }(p):=\underset{v\in {\mathbb{R}}^n}{\sup }\{⟨p,v⟩-L(v)\}$$

Our conditions ensures that there exists a point of maximum, call it $v^{\ast }$. Provided that $L(v)$ is differentiable at $v^{\ast }$, imposing stationarity one finds

$$p=D_{v}L(v^{\ast })$$

so that this equation is solvable (perhaps not uniquely) for $v^{\ast }=h(p)$. Then

$$L^{\ast }(p)=h(p)p-L(h(p))$$

Duality of the Legendre transform §

Theorem The new function $p\mapsto L^{\ast }(p)$ is

• convex;
• ${\lim }_{|v|\to \infty }\frac{L^{\ast }(v)}{|v|}=+\infty$
• $L^{\ast \ast }=L$ is involutive.

Proof For each fixex $v$ the function $pv-L(v)$ is linear, so that the $\sup$ is convex:

$$L^{\ast }(\alpha p_1+(1-\alpha )p_2)=\underset{v}{\sup }\alpha p_{1}v+(1-\alpha )p_{2}v-L(v)$$ $$\le \alpha \underset{v}{\sup }\{p_{1}v-L(v)\}+(1-\alpha )\underset{v}{\sup }\{p_{2}v-L(v)\}=\alpha L^{\ast }(p_1)+(1-\alpha )L^{\ast }(p_2)\square$$

From Velenik and Friedli §

Def (Legendre-Fenchel transform) Let $f:I\to \mathbb{R}\cup \{+\infty \}$. The Legendre transform of $f$ is defined by:

$$f(y{)}^{\ast }:=\underset{x\in I}{\sup }\{yx-f(x)\}$$

Geometrically: the maximum distance between the line $yx$ and the function graph.

Proposition The legendre transform of any function is convex. Proof $\forall \alpha \in [0,1]$

$$f^{\ast }(\alpha y_1+(1-\alpha )y_2)=\underset{x}{\sup }\{\alpha y_{1}x+y_{2}x-\alpha y_{2}x-f(x)\}$$

adding and subtracting $\alpha f(x)$

$$\le \alpha f^{\ast }(y_1)+f^{\ast }(y_2)-\alpha f^{\ast }(y_2)\square$$

Oss This implies that if $f$ is not convex, $(f^{\ast }{)}^{\ast }\ne f$ i.e. that the Legendre Transform is not involutive.

Def (Supporting line) A supporting line at $x$ with slope $m$ for the function $f$ is a line such that:

$$f(y)\ge f(x)+m(y-x)$$

Oss A function is convex iff every point admits (at least one) supporting line. Oss If a convex function is non differentiable at $x$, then it has infinite supporting line at this point with slopes in $[{\partial }^{-}f(x),{\partial }^{+}f(x)]$.

Proposition (Duality of supporting lines slopes and points) If $f$ admits a supporting line with slope $k$ at point $x_0$, then $(k,f^{\ast }(k))$ admits a supporting line with slope $x_0$. Proof

$$f^{\ast }(k)+x_0(z-k)=\underset{x}{\sup }\{kx-f(x)+x_{0}z-x_{0}k\}$$

since $f$ admits a supporting line at $x_0$ with slope $k$

$$f(x)\ge f(x_0)+k(x-x_0)⟹-k{x}_0\le f(x)-f(x_0)-kx$$

so that

$$\le \underset{x}{\sup }\{kx-f(x)+x_{0}z+f(x)-f(x_0)-kx\}=x_{0}z-f(x_0)\le f^{\ast }(z)$$

so $f^{\ast }$ admits a supporting line at $k$ with slope $x_0$. $\square$

**Non differentiable points

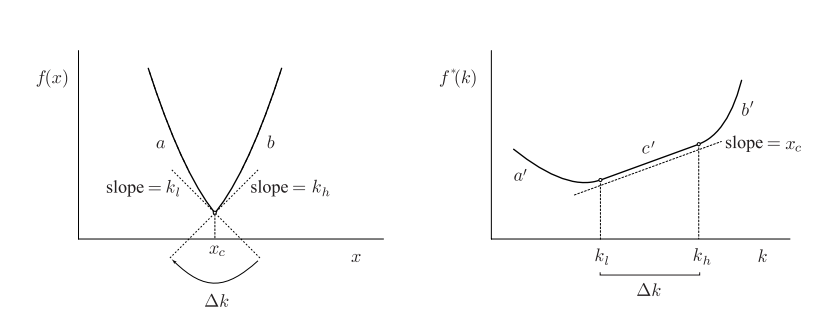
Proposition Let $f$ be a convex function. Then:

1. If $f$ is not differentiable at $x$, $f^{\ast }$ is affine in the interval $[{\partial }^{-}f(x),{\partial }^{+}f(x)]$;
2. If $f$ is affine in some interval $[a,b]$ with slope $k$, then $f^{\ast }$ is not differentiable in $k$ and ${\partial }^{-}{f}^{\ast }(k)\ge b>a\ge {\partial }^{-}{f}^{\ast }(k)$.

Proof Since $f$ is convex, at the point $x$ it admits infinite supporting lines with slopes in $[{\partial }^{-}f(x),{\partial }^{+}f(x)]$. By the prevoious propositipon $f^{\ast }$ admits at al point $[{\partial }^{-}f(x),{\partial }^{+}f(x)]$ a supporting line with slope $x$. Since $f^{\ast }$ is convex, all the supporting line coincide, and $f^{\ast }$ is affine in this interval. $\square$