Mc Culloch Pitts neuron §

E’ un modello matematico semplificato dei complicati modelli differenziali dei Biological neurons. Introdotto nel 1943, chiamato anche formal neuron, in breve:

the formal neuron receives a series of inputs from adjacent neurons and generates an output that results from the sum of the inputs, each of which is weighed by a factor that takes into account the functioning of the related synapses

Assumiamo che un neurone ed i suoi $N$ neuroni vicini (collegati da sinapsi) ciascuno con uno stato possibile $S_i$ che insieme formano lo stato della rete $S=\{S_1,\dots ,S_N\}$, ed un insieme di pesi sinaptici $J=\{J_1,\dots J_N\}$, allora l’output del neurone è determinato da:

$$y=\Theta \left(\sum _{i=1}^N{J}_i{S}_i-U^{\ast }\right)$$

$U^{\ast }$ viene detta soglia di attivazione, se il potenziale presinaptico definito come:

$$U:=\sum _{i=1}^N{J}_i{s}_i$$

è minore di $U^{\ast }$ l’uscita è nulla (quiescient state), per la funzione di Haveside, $y=1$ in caso contrario (active state).

Se vogliamo costruire reti collegando questi neuroni, allora l’uscita è anche l’insime degli stati, quindi $S=\{0,1{\}}^N$. Se pensiamo ad una rete allora definiamo una matrice di interazioni $J_{i,j}$, quindi per ogni neurone vale:

$$S_i=\Theta \left(\sum _{i=1}^N{J}_{ij}{S}_j-U_i^{\ast }\right)$$

notiamo che possiamoa vere interazioni non simmetriche $J_{ij}\ne J_{ji}$ ed autointerazioni $J_{ii}\ne 0$.

Universalità dei neuroni MP §

Every finite digital machine can be regarded as a device that maps finite-dimensional binary input vectors $S\in \Omega \subseteq \{0,1{\}}^N$ (could be a partial function that doesn’t terminate!) in a finite string with the same alphabet $S^{\prime }\in \{0,1{\}}^N$.

Then every finite deterministic digital machine can be specified in full by specifying the output vector for every possible input vector, that is, by specifying the mapping $M$:

$$M:\Omega \mapsto \{0,1{\}}^{K}MS=S^{\prime }\forall S\in \Omega$$

Possiamo scomporre la mappa in $K$ mappe indipendenti con stesso input ma solo un bit in uscita:

$$M_l:\Omega \mapsto \{0,1\}{M}_{l}S=S_l^{\prime }\forall S\in \Omega l=1,\dots ,K$$

We conclude that we are allowed to concentrate only on the question of whether it is possible to perform any single-output mapping M : Ω ⊆ {0, 1} N → {0, 1} with networks of MP neurons.

we first introduce a partitioning of the set $\Omega$ of input vectors into two subsets, depending on the corresponding desired output value:

$$\Omega ={\Omega }^{+}\cup {\Omega }^{-}$$ $${\Omega }^{+}:=\{S\in \Omega |MS=1\}{\Omega }^{-}:=\{S\in \Omega |MS=0\}$$

Quindi le macchine $M_l$ devono capire se l’input $S$ è nel sottoinsieme giusto, ovvero $S\in {\Omega }^{+}$ oppure $S\in {\Omega }^{-}$. Chiamiamo $S^{\mu }$ gli elementi di $\Omega$ che applicati ad $M_l$ danno in uscita il bit $1$. Quindi quello che deve fare la rete, è dato un input $S$ controllare se $S\in {\Omega }^{+}$, ovvero se è uguale a qualche elemento: $\exists S^{\mu }\in {\Omega }^{+}$ tale che $S=S^{\mu }$. se è così, restituisce uno, zero altrimenti. Questa cosa si può fare facilmente con operazioni binarie elementali, infatti se $S^{\mu }=S$, sono uguali bit a bit, un and:

$$SAME(X,Y)⟺{\wedge }_{i=1}^N\left[(X_i\wedge Y_i)\vee \neg (X_i\vee Y_i)\right]$$

quindi:

$$S\in {\Omega }^{+}⟺{\vee }_{\mu =1}^P{\wedge }_{i=1}^N\left[(S_i\wedge S_{{\mu }_i})\vee \neg (S_i\vee S_{{\mu }_i})\right]$$

Le $3$ operazioni logiche usate sono ovviamente realizzabile con delle reti di neuroni $MP$:

• $NOT$

$$\neg X=\Theta (1/2-X)$$

• $OR$

$$X\vee Y=\Theta (X+Y-1/2)$$

• $AND$

$$X\wedge Y=\Theta (X+Y-3/2)$$

Osservazione Un solo layer non può nemmeno fare tutte le operazioni binarie, non esiste per lo $XOR$. Il motivo geometrico è chiari: non sono linearmente separabili!

$XOR(X,Y)\equiv NOTAND(X,Y)ANDOR(X,Y)$

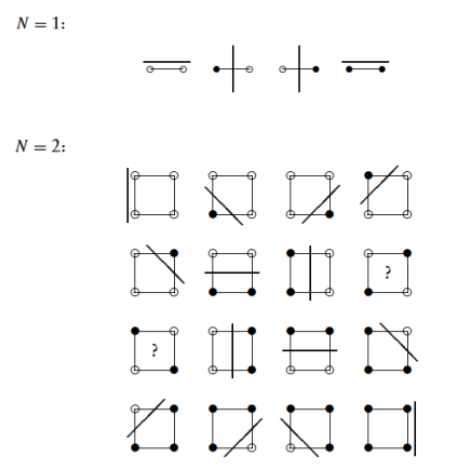
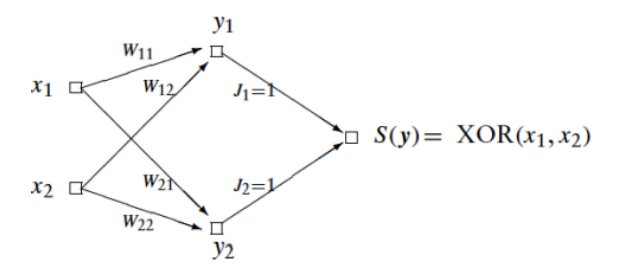
Quindi bastano due layer per replicare lo $XOR$. In realtà vale il claim forte:

Teorema bastano 2 layer §

Ogni funzione $M:\{0,1{\}}^N\mapsto \{0,1\}$ può essere rappresentata da una reta di solo due layer.

Proof §

L’idea è molto semplice, il livello nascosto contiene un neurone per ogni configurazione dentro ${\Omega }^{+}$. Il compito di questi neuroni è accendersi se riconoscono una certa configurazione. Non ci resta quindi che mettere un singolo neurone finale di $OR$.

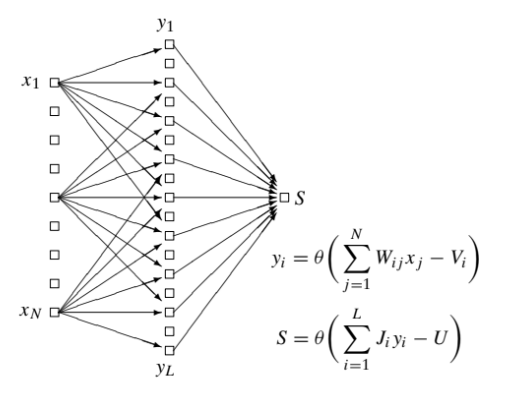
La questione è quindi costruire i neuroni dell’hidden layer. Definiamo una funzione building block con la proprietà voluta:

$$G(x,x^{\ast })⟺x=x^{\ast }$$

claim la funzione:

$$G(x,x^{\ast }):=\Theta \left(\sum _{i=1}^N(2x_i-1)(2x^{\ast }-1)-N+1\right)$$

fa quello che voglio.

• Se $x^{\ast }=x$

$$\Theta \left(\sum _{i=1}^N(2x_i-1{)}^2-N+1\right)$$

vale:

$$\sum _{i=1}^N(2x_i-1{)}^2=N$$

quindi

$$\sum _{i=1}^N(2x_i-1{)}^2-N+1=1$$

concludendo che $G(x,x^{\ast })=1$.

• Al contrario quando $x\ne x^{\ast }$, i corrispondente termini nella sommatoria valgono:

$$(2x_i-1)(2x_i^{\ast }-1)=\{\begin{array}{l}1\text{ se }{x}_i=x_i^{\ast }\\ -1\text{ se }{x}_i\ne x_i^{\ast }\end{array}$$

di conseguenza la somma vale:

$$\#\text{indici uguali}-\#\text{indici diversi}=N-2\#\text{indici divesi}$$

quindi nell funzione theta ho:

$$N-2\#\text{ind.div.}-N+1=1-2\#\text{ind.div.}<0$$

perchè per ipotesi almeno un indice è divetso, quindi $G(x,x^{\ast })=0$. $\square$

Ovviamente fissato $x^{\ast }$ la funzione $G(x)$ può essere rappesentata da un neurone $MP$, basta espandere il prodotto, ho termini lineari in $x_i$ ed altri costanti.

La rete finale avrà dunque i parametri:

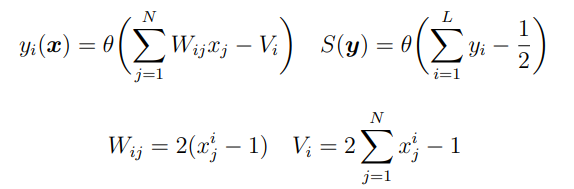
Remaks §

• Il numero di neuroni necessari per il livello nascosto $L$ può scalare con le dimensioni dello spazio $\Omega$, ovvero è esponenziale in N ($\sim 2^N$)
• concatenando le varie reti per ogni bit, otteniamo sempre una rete a due layer.
• Perfect knowledge of the function $M$ allowed us to determine the set of weights which makes the network to exactly emulate $M$. In real situations the scenario is different: only a sample of input-output pairs is available and, based on these, we have to infer the “optimal” (according to some cost function) configuration for weights which makes the network to emulate the operation M at least on the basis of the available knowledge. In order to find this setting one introduces learning rules, namely iteractive evolution rules to tune weights.

Dinamica §

Possiamo introdurre una dinamica discreta tra stati di una rete $S(t)$:

$$S_i(t+\Delta t)=\Theta \left(\sum _{j=1}^N{J}_{ij}{S}_j(t)+U_i^{\ast }\right)$$

Si può pensare a $\Delta t$ come un tempo refrattario dei neuroni biologici.

Ci sono due maniera di realizzare questa dinamica:

• Dinamica parallela Gli stati evolvono tutti insiemi;
• Dinamica sequenziale Si sceglie un neurone $i$ e si aggiorna solo quello.

Stocasticità §

Introduciamo delle perturbazioni random sulla soglia di attivazione, sommando una variabile a media nulla:

$$U_i^{\ast }(t)=U_i^{\ast }+\frac{1}{2}T{z}_i(t)$$

dove $\frac{1}{2}T$ è la deviazione standard, $z(t)$ una variabile a media nulla e varianza unitaria. Il parametro $T$ controlla dunque il grado di stocasticità (una temperatura).

Effettuiamo anche in cambio da $S_i=\{0,1\}$ a spin ${\sigma }_i=\{1,-1\}$. La regola di update diventa:

$${\sigma }_i(t+\Delta t)=sign\left[{\phi }_i(t)+T{z}_i(t)\right]{\phi }_i(t)=\sum _{j=1}^N{J}_{ij}{\sigma }_j(t)+h_i$$

da qui si capisce il fattore $1/2$ aggiunto al rumore. La quantità $\phi (t)$ viene detto campo locale.

La probabilità di trovare un neurone nello stato ${\sigma }_i=1,-1$ al tempo $t+\Delta t$ è dunque una variabile aleatoria che dipende dalle v.a. $z_i(t)$ e dallo stato della rete $\sigma (t)$. Se supponiamo sia simmetrico:

$$\mathbb{P}[{\sigma }_i(t+\Delta t)=1]=\mathbb{P}[{\phi }_i(t)>-T{z}_i(t)]={\int }_{{\phi }_i(t)/T}^{\infty }\mathbb{P}[z_i(t)=z]dz$$ $$\mathbb{P}[{\sigma }_i(t+\Delta t)=-1]=\mathbb{P}[{\phi }_i(t)<-T{z}_i(t)]={\int }_{-\infty }^{-{\phi }_i(t)/T}\mathbb{P}[z_i(t)=z]dz$$

esprimento il tutto in funzione della cumulativa $g(x)$

$$\mathbb{P}[{\sigma }_i(t+1)=\pm 1]=g(\pm {\phi }_i(t)/T)$$

Con $z_i(t)\sim N(0,1)$ la cumulativa è $erf(x)$; un’altra scelta simile è la tangente iperbolica:

$$g(x)=\frac{1}{2}\left(1-\tanh (x)\right)$$

a cui corrisponde un rumore distribuito come:

$$\mathbb{P}[z_i(t)=x]=\frac{1}{2}\left(1-{\tanh }^2(x)\right)$$

Per la dinamica parallela, supponendo le variabili indipendenti, la probabilità fattorizza e si ottiene:

$$\mathbb{P}(\sigma (t+1))=\prod _{i=1}^N\mathbb{P}({\sigma }_i(t+1)=\pm 1)=\prod _{i=1}^{N}g({\sigma }_i(t+1){\phi }_i(t)/T)$$

Noiseless recurrent networks §

Studiamo la dinamica nel caso $T=0$ noiseless per i casi

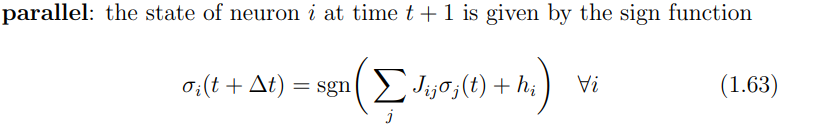
Parallel dynamics §

Es 1 Caso banale: $J_{ij}=0$ e $h_i\ne 0$. La regola di update è banale, non dipende dallo stato precedente, dopo una iterazione tutto il sistema va nello stato finale:

$${\sigma }_i=sign(h_i)$$

Il bacino di attrazione per questo stato punto fisso è tutto il dominio $\mathcal{D}=\{-1,1{\}}^N$. Es 2 Supponiamo ora $J_{ij}=\frac{J}{N}$ e $h_i=0$, ovvero interazioni simmetriche e campo esterno nullo. Otteniamo la regola di update: 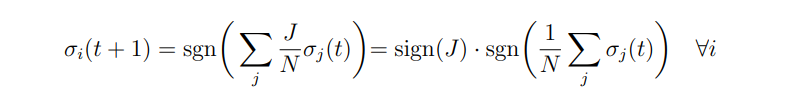Notiamo come compare un’osservabile macroscopica, la magnetizzazzione media (spin medio):

$$m(t):=\frac{1}{N}\sum _{i=1}^N{\sigma }_i(t)$$

Possiamo ottenere una formula di update per questa osservabile macroscopica sommando:

$$m(t+1)=\frac{1}{N}\sum _{i=1}^N{\sigma }_i(t+1)=\frac{sign(J)}{N}\sum _{i=1}^{N}sign(m(t))=sign(J)\cdot sign(m(t))$$

Se $J>0$, abbiamo una dinamica imitatoria: i neuroni tendono a fare quello che fanno gli altri. Partizioniamo le configurazioni in:

$${\mathcal{D}}^{+}:=\{\sigma \in \{-1,1{\}}^N:m(\sigma )>0\}{\mathcal{D}}^{-}:=\{\sigma \in \{-1,1{\}}^N:m(\sigma )<0\}$$

(supponiamo di avere un numero dispari di neuroni, così non abbiamo il caso patologico $m=0$).

Abbiamo punti fissi $\{-1,-1,\dots {\}}^N$ e $\{+1,\dots ,+1{\}}^N$ che corrispondono a $m=-1$ e $m=1$.

Se $J<0$ abbiamo un ciclo limite di periodo due tra stati $m=1$ ed $m=-1$.

Es 3 Caso $J_{ij}=\frac{J}{N}$ e $h_i=h\ne 0$. La regola di update della magnetizzazzione media è:

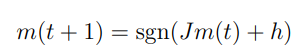
Se il campo esterno $h$ è troppo forte, ovvero $|h|>|J|$ otteniamo una dinamica banale, come nel caso senza interazioni.

Con $J>0$ otteniamo sempre due punti fissi, ma con bacini d’attrazione non uguali e che dipendono dal rapporto $\frac{h}{J}$.

Con $J<0$ otteniamo sempre un ciclo di periodo due, $\frac{h}{J}$ controlla quanto ci metto a raggiungere il ciclo.

Sequential dynamics §

Studiamo gli stati limite tramite Funzioni di Lyapunov.

Proposizione Se abbiamo interazioni simmetriche $J_{ij}=J_{ji}$, ed autointerazioni non negative $J_{ii}\ge 0$, un campo esterno $h_i$ e noisless ($T=0$), allora

$$L(\sigma ):=-\frac{1}{2}\sum _{i,j}{J}_{ij}{\sigma }_i{\sigma }_J-\sum _i{h}_i{\sigma }_i$$

è una funzione di Lyapunov della dinamica sequenziale:

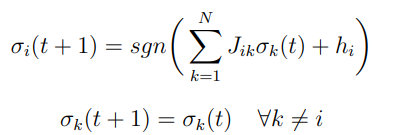
dove si estrae $i$ uniformemente in $[1,N]$.

Durante la dinamica la funzione evolve:

$$\Delta L=L(\sigma (t+1))-L(\sigma (t))=-2\left|\sum _{j=1}^N{J}_{ij}{\sigma }_j+h_i\right|-2J_{ii}\le 0$$

Siccome $L(\sigma )$ è limitata inferiormente, ammette un minimo ed il sistema arriverà a queste configurazioni e si fermerà. (Richiediamo distanza di hamming $1$).

Pattern retrival §

Possiamo vedere questa abilità delle reti di “ricordare” informazioni $\sigma (\infty )$, dato un input iniziale $\sigma (0)$, sfruttando questa dinamica verso attrattori.

Basando sulla regola (principio) di Hebb:

Neurons that fire together wire together Neurons out of sync fail to link

Risulta ragionevole: 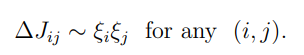Si vede facilmente che possiamo memorizzare singoli pattern $\xi$ definendo le connessioni in accordo con la regola di Hebb. Aggiungere campo esterno complica le cose, valgono le stesse considerazioni fatte nella dinamica parallela caso $J$ simmetrico con campo esterno. Quindi la rete avrà punti fissi in $\xi$ e $-\xi$, a seconda di $\frac{h}{J}$.

Per più pattern, una scelta ragionevole è mediare: 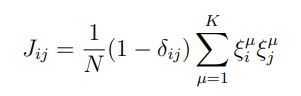Per semplificare la trattazzione assumiamo che i pattern siano ortogonali.

Proposizione La dinamica sequenziale applicata ad una rete con pesi dati dalla regola di Hebb e $h_1=0$, mostra $2K$ stati stazionari, che corrispondono ai pattern ed hai loro inversi.

Dim Scriviamo la funzione di Lyapunov:

$$L(\sigma )=-\frac{1}{2}\sum _{ij}{J}_{ij}{\sigma }_i{\sigma }_j+-\sum _i{\sigma }_i{h}_i$$

con la regola di Hebb e campi esterni nulli

$$=\frac{1}{2N}\sum _{ij}({\delta }_{ij}-1)\left[\sum _{\mu =1}^K{\xi }_i^{\mu }{\xi }_j^{\mu }\right]{\sigma }_i{\sigma }_j$$ $$=\frac{1}{2N}\sum _{ij}\left[\sum _{\mu =1}^K{\xi }_i^{\mu }{\xi }_j^{\mu }\right]{\sigma }_i{\sigma }_j+\frac{1}{2}K$$

notando che

$${\left(\sum _{i=1}^N{\xi }_i^{\mu }{\sigma }_i\right)}^2=\sum _{ij}{\xi }_i^{\mu }{\xi }_j^{\mu }{\sigma }_i{\sigma }_j$$

dunque

$$L(\sigma )=-\frac{1}{2}\sum _{\mu =1}^K{\left(\frac{1}{\sqrt{N}}\sum _{i=1}^N{\xi }_i^{\mu }{\sigma }_i\right)}^2+\frac{1}{2}K$$

Il termine al quadrato non è altro che il prodotto scalare tra lo stato ed il pattern (normalizzato) ${\xi }_i$. Siccome abbiamo supposto per ipotesi che i pattern sono ortogonali, per massimizzare il prodotto scalare $\sigma$ deve avere la stessa direzione di $\xi$, ed in questo caso $⟨\xi ,\sigma ⟩=\pm \Vert \sigma \Vert$ e zero per gli altri pattern, dunque:

$$L(\sigma )\ge \frac{1}{2}K-\frac{1}{2}N$$

ed il minimo si ottiene quando $\sigma =\pm \xi$.

Osservazione Non è vero che tutti i minimi sono pattern, esistono dei minimi spuri.

$${\sigma }_i=sgn({\xi }_i^1+{\xi }_i^2+\dots )$$

Proposizione Misture dispari dei pattern sono stati stazionari. Misture pari sono stati stazionario instabili. Sono minimi locali.

Domande §

1. Capacità della rete? (in funzione di $N$)
2. Training migliore?
3. Utilità del random noise?