Metodo delle caratteristiche

Method of characteristics §

Metodo usato per risolvere PDE del primo ordine, (si può estendere alle PDE iperboliche). Il metodo riduce la PDE in una famiglia di EDO, le cui soluzione sono dette curve caratteristiche attraverso le quali si risolve la PDE grazie alla condizione inziale.

General case §

Consider ther general non-linear first order PDE

$$F(Du,u,x)=0\text{ in }U$$

subject to the boundary condition

$$u=g\text{ on }\Gamma \subseteq \partial U$$

suppose that $F,g$ are smooth functions. The plan is to reduce the PDE to a system of ODEs. Let $s\in I\subseteq \mathbb{R}$ define the curve

$$z(s):=u(x(s))$$

where $u$ is a $C^2$ solution to our PDE. Set

$$p(s):=Du(x(s))$$

our task is to find a clever curve $x(s)$ that allows us to compute $p$ and $z$. Differentiating $p(s)$

$${\dot{p}}_i(s)=\sum _{j=1^n}{u}_{x_i{x}_j}(x(s)){\dot{x}}_j(s)$$

Now differentiate the PDE w.r.t $x_i$

$$\sum _{j=1}{F}_{p_j}(Du,u,x)u_{x_j{x}_i}+F_z(Du,u,x)u_{x_i}+F_{x_i}(Du,u,x)=0$$

we can use this idenity to compute the termi with $u_{x_i{x}_j}$, provided that

$${\dot{x}}_j(s)=F_{p_j}(Du,u,x)$$

using our definitions, and the last identity

$${\dot{p}}_i(s)=-F_z(p(s),z(s),x(s))p_i(s)-F_{x_i}(p(s),z(s),x(s))$$

we are missing and equation for $\dot{z}(s)$, so let’s compute this

$$\dot{z}(s)=\sum _{j=1}{u}_{x_j}(x(s)){\dot{x}}_j(s)=\sum _{j=1}{p}_j(s)F_{p_j}(p(s),z(s),x(s))$$

which can be writtens as a scalar product. Summarizing our results in vector notation:

$$\{\begin{array}{l}\dot{\mathbf{p}}(s)=-F_z(\mathbf{p}(s),z(s),x(s))\mathbf{P}(s)-D_{x}F(\mathbf{p}(s),z(s),x(s))\\ \dot{z}(s)=\mathbf{p}(s)\cdot D_{p}F(\mathbf{p}(s),z(s),x(s))\\ \dot{\mathbf{x}}(s)=D_{p}F(\mathbf{p}(s),z(s),x(s))\end{array}$$

We are still missing initial conditions. Imagine our characateristics starting from a point $x_0\in \Gamma$. We assume to have a “flat” boundary, so that for any given point the boundary is just the plane $x_n=0$.

Then we set $x(0)=x_0$, it follows from the boundary conditions that $z(0)=g(x_0)$ and that $p_i(0)=g_{x_i}(x_0)$ $i=1,\dots ,n-1$, and since we want the PDE to hold $F(p_0,z_0,x_0)=0$. Note that $z_0$ is uniqueley determined by our choice $x_0$, but the vector ${\mathbf{p}}_0$ is not guaranteed to exists, or be unique.

Linear case §

Risolviamo l’equazione:

$${\partial }_{t}u+{\partial }_x[a(x)u]=0$$

in forma semi-lineare diventa:

$$\{\begin{array}{l}{\partial }_{t}u+a(x){\partial }_{x}u=-ua(x{)}^{\prime }\\ u(0,x)=u_0(x)\end{array}$$

che ha come caso particolare l’equazione linear advection.

Proof L’idea fondamentale è supporre che la seconda variabile sia dipendente dal tempo $(t,x(t))$, effettuando la derivata totale di $u$ si ottiene:

$$\frac{du}{dt}={\partial }_{t}u+\dot{x}{\partial }_{x}u$$

confrontando con l’equazione, se imponiamo che $\dot{x}=a(x)$ siccome $u$ risolve l’equazione, la derivata totale nel tempo lungo le caratterische è $-ua(x{)}^{\prime }$, il termine di sorgente. Stiamo dicendo che se mi muovo lungo queste curve, il valore di $u$ è regolato da una EDO. Per trovare $u$ al tempo e posizione generica, mi basta trovare quale caratteristica passa per quel punto.

1. trovare le caratteristiche, risolvendo un’EDO:

$$\dot{x}(t)=a(x),x(0)=x_0$$

2. ricostruire la soluzione partendo dalla condizione iniziale risolvendo un’altra EDO:

$$\frac{d}{dt}u(t,x(t))=-a^{\prime }(x)u(t,x(t))$$

Risolviamo esplicitamente nel caso della linear advection, quindi $a(x)=a\in \mathbb{R}$ costante. Il punto 1 è una semplice integrazione, e l’edo 2 è banale: la u resta costante lungo le caratteristiche.

$$u(t,x(t))=u(0,x(0))=u_0(x_0)=u_0(x-at)$$

la soluzione trasla con velocità $a$ la condizione iniziale, se $a>0$ verso destra.

Nel caso quasi lineare in cui $a(u)$ è

Condizioni di bordo §

Da notare che se studiamo la funzione in sottoinsiemi di $\mathbb{R}$ la condizione iniziale $u_0(x)$ potrebbe non bastare a chiudere il problema. Supponiamo di lavorare nella semiretta $x\ge 0$ e $a>0$, abbiamo una regione dove non passa nessuna curva caratteristica: Dobbiamo aggiungere il valore di $u$ sul “bordo” per ogni tempo:

$$u(t,0)=g(t)$$

Se invece $a<0$ non abbiamo problemi: 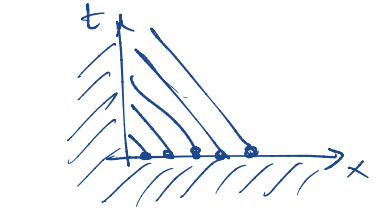Ovviamente per $x<0$ siamo nel caso opposto.

Se lavoro con intervalli finiti, es $[0,L]$ avrò sempre un lato dove devo specificare il valore di $u$ ad ogni istante.

Con queste condizioni il problema è ben posto: la soluzione è unica.

Una soluzione alternativa è usare condizioni al bordo periodiche!

dim unicità §

dimostriamo l’unicità per il caso $a>0$ nell’intervallo $[0,L]$. Usiamo un metodo dell’energia: moltiplicare l’equazione per una funzione/derivata di $u$ ed integrare per ottenere una uguaglianza/disuguaglianza. Moltiplichiamo la PDE per $u$:

$$u{\partial }_{t}u+au{\partial }_{x}u=\frac{1}{2}{\partial }_t{u}^2+\frac{a}{2}{\partial }_x{u}^2=0$$

Moltiplichiamo per 2 ed integriamo nello spazio sull’intervallo:

$$\frac{d}{dt}{\int }_0^L{u}^{2}dx+a[u^2(t,L)-u^2(t,0)]=0$$

ma $u^2(t,0)=g^2(t)$, il dato di bordo (sinitro, siamo nel caso $a>0$).

$$\frac{d}{dt}{\int }_0^L{u}^{2}dx=a[-u^2(t,L)+g^2(t)]\le a{g}^2(t)$$

perchè abbiamo rimosso la quantità negativa $-a{u}^2$. Integriamo nel tempo tra $0$ e $t$:

$${\int }_0^{L}u(t,x{)}^{2}dx-{\int }_0^{L}u(0,x{)}^{2}dx\le a{\int }_0^t{g}^2(s)ds$$

ma $u(0,x{)}^2=u_0(x{)}^2$ la condizione iniziale (cambito la variabile muta in $s$ per comodità).

Mostriamo che date due soluzioni del problema con uguali condizioni iniziali e di bordo sono uguali tra loro. Sfruttiamo la linearità del problema: la differenza è soluzione, con condizioni al bordo differenza, usiamo la disequazione integrale ottenuta:

$${\int }_0^L(u_1(t,x)-u_2(t,x){)}^{2}dx\le {\int }_0^L(u_{01}(x)-u_{02}(x){)}^{2}dx+a{\int }_0^t(g_1(s)-g_2(s){)}^{2}ds$$

Se le condizioni inziali sono le stesse si ottiene:

$$0\le {\int }_0^L(u_1(t,x)-u_2(t,x){)}^2\le 0$$

L’integrale è ovviamente maggiore uguale a zero. Siccome per ipotesi $u\in C^1$, concludiamo che:

$$u_1(t,x)=u_2(t,x)$$

$QED$

Caso quasi-lineare §

Interessante è il caso quasi-lineare:

$${\partial }_{t}u+a(u){\partial }_{x}u=0$$

per il quale vale il seguente teorema:

Teorema §

Supponiamo che $u\in C^1[0,T]\times \Omega$ sia una soluzione in una regione $\Omega \subset {\mathbb{R}}^n$, la funzione $a\in C^1$. Allora per ogni $x_0\in \Omega$, $u$ è costante lungo le curve caratteristiche definite da:

$$x(t)=x_0+a(u(0,x_0))t$$

Osservazione §

Il teorema assume per ipotesi che esista $u\in C^1$ soluzione, ciò non è sempre possibile, le caratteristiche possono intersecarsi in un tempo finito (nel caso non lineare) e generare discontinuità nella soluzione: si parla di soluzioni in senso debole. Ciò avviene nel modello LWR del traffico, si possono generare onde di shock (dicontinuità che si propaga).