Riduzione polinomiale Sia una formula CNF. Costruiamo un grafo 3-colorabile se e solo se è SAT.
L’idea è che i colori simboleggeranno l’assegnamento, ma ne abbiamo 3 e non 2 (True False). Il terzo colore “in più” è fondamentale (la 2-colorabilità è risolvibile in tempo lineare). Per ogni letterale includiamo un vertice, e colleghiamo i letterali complementari tra di loro e con un terzo vertice. Dovranno avere colori diversi: è questo lo scopo del gadget, escludere assegnamenti illegali.
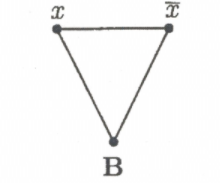Per ogni clausola in includiamo il seguente sottografo:
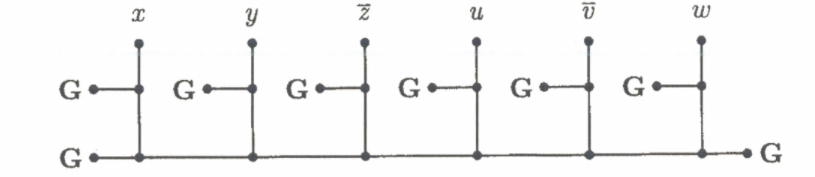associato alla clausola . Con indichiamo lo stesso vertice. Questo sottografo è 3-colorabile se e solo se almeno uno dei vertici è verde (True). Abbiamo costruito l’OR logico.
Se tutti i vertici dei letterali sono colorati Rossi, allora in mezzo sono Blu, quindi sotto si alternano R, G, R ecc.
- Se k è pari (come nella figura) pongo entrambi gli estremi a G
- Se k è dispari pongo il veritice di destra a R E’ una situazione simile alla riduzione SAT to 3SAT, si crea un serpentello obbligato, una catena di implicazioni che può essere spezzata solo se una letterale è true (in questo caso abbiamo piena libertà sul vertice subito adiacente sotto.