Sensitivity of eigenvalue problems §

Given a matrix $A\in {\mathbb{C}}^{n\times n}$ we know that a new matrix obtained via a Similarity transformation has the same eigenvalues. When computing numerically the eigenvalue of a given matrix, it will be convinient to transform the starting matrix in a more simple form using similarity transformation to preserve the spectrum. The following question arises:

If we perturb the starting matrix $A$ with $\delta A$, how much this will impact the spectrum?

Consider a diagonalizable matrix $A$. This means there exists an invertivle matrix $V$ sush that:

$$V^{-1}AV=D$$

Where $D$ is diagonal. Since this is a similarity transformation, the diagonal values are the spectrum of $A$. We now study theoretically the perturbed problem:

$$V^{-1}(A+\delta A)V=D+E$$

Where $E=V^{-1}\delta AV$.

This still is a similarity transformation, hence $A+\delta A$ and $D+E$ share the same eigenvalues.

Call the unperturbed eigenvalues ${\lambda }_i$, the perturbed ${\mu }_i$. Our goal is to exstimate the difference $|{\lambda }_i-{\mu }_i|$.

Consider the eigenvector of the perturbed system:

$$(D+E)w=\mu w$$

rearrenging this

$$w=(\mu I-D{)}^{-1}Ew$$

we now take norms, using basic propriety of induced matrix norms we get the inequality:

$$1\le \Vert (\mu I-D{)}^{-1}{\Vert }_2\Vert E{\Vert }_2$$ $$\Vert (\mu I-D{)}^{-1}{\Vert }_2^{-1}\le \Vert E{\Vert }_2$$

the matrix $(\mu I-D{)}^{-1}$ is just a diagonal matrix whose nonzero entries are:

$$\frac{1}{{\mu }_i-{\lambda }_i}$$

the 2-norm is just the biggest diagonal absolute value. Call this $\frac{1}{|\mu -\lambda |}$. Then:

$$|\mu -\lambda |\le \Vert E{\Vert }_2=\Vert V^{-1}\delta AV{\Vert }_2\le {\mathcal{K}}_2(V)\Vert \delta A{\Vert }_2$$

This is result is knows as Bauer-Fike theorem.

Remark If $A$ and $\delta A$ are normal, then $V$ is unitary and ${\mathcal{K}}_2(V)=1$.

Bauer-fike theorem §

Let $A$ be a diagonalizable matrix, and $\delta A$ such that $A+\delta A$ is still diagonlaizable. Let $\mu$ be an eigenvalus of $A+\delta A$, then there exists $\lambda$, eigenvalue of $A$ such that:

$$|\lambda -\mu |\le {\mathcal{K}}_p(V)\Vert \delta A{\Vert }_p$$

Remaks In short, this theorm gives us a bound on the distance of the perturbed eigenvalues from a suitable unperturbed eigenvalue.

However it doesn not tell us in wich disk the pertubed eigenvalue are contained, it can happen that they are close to the same unperturbed eigenvalues:

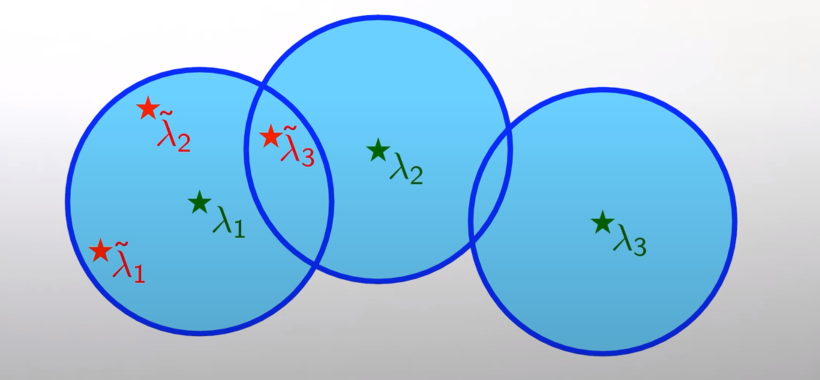
Weyl’s theorem §

In the case where $A$ and $A+\delta A$ are hermitian, we have a stronger result.

Let ${\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_n$ and ${\mu }_1\le {\mu }_2\le \cdots \le {\mu }_n$ the (real) eigenvalues of $A$ and $A+\delta A$, respectively. Then ${\max }_{i=1,\dots ,n}|{\lambda }_i-{\mu }_i|\le \Vert \delta A{\Vert }_2$.