Hitting probability and mean hitting times

Let $(X_n{)}_{n\ge 0}$ be a Markov chain with transition matrix $P$. The first hitting time of a subset of states $A\subseteq I$ is the random variable $H^A:\Omega \to \mathbb{N}\cup \{\infty \}$ defined by

$$H^A=\inf \{n\in \mathbb{N}:X_n\in A\}$$

with the usual convenction that the infimum of the empty set is $\infty$. Remark Note that it’s a stopping time.

The probability starting from state $i$ that $(X_n{)}_{n\ge 0}$ ever hits $A$ is

$$h_i^A:={\mathbb{P}}_i(H^A<\infty )$$

when $A$ is a closed class, $h_i^A$ is called an absorption probability.

The mean hitting time for $(X_n{)}_{n\ge 0}$ reaching $A$ is given by

$$k_i^A:={\mathbb{E}}_i(H^A)=\sum _{n\ge 0}n{\mathbb{P}}_i(H^A=n)+\infty {\mathbb{P}}_i(H^A=\infty )$$

Computing $h_i^A$ and $k_i^A$ §

Consider the example

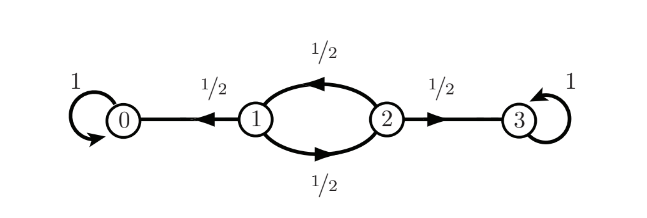
it’s a $4$ state Markov chain with absorbing states $0$ and $3$. Let $h_i={\mathbb{P}}_i(\text{hit }3)$ and $k_i={\mathbb{E}}_i(\text{time to hit }\{0,3\})$. Clearly,

• $h_0=0$
• $h_1=\frac{1}{2}{h}_0+\frac{1}{2}{h}_2$
• $h_2=\frac{1}{2}{h}_1+\frac{1}{2}{h}_3$
• $h_3=1$

and

• $k_0=0$
• $k_1=1+\frac{1}{2}{k}_0+\frac{1}{2}{k}_2$
• $k_2=1+\frac{1}{2}{k}_1+\frac{1}{2}{k}_3$
• $k_3=0$ these linear systems can be solved to obtain $h_1=1/3$, $h_2=2/3$ and $k_1=k_2=2$.

Theorem The vector of hitting probabilities $h^A=(h_i^A{)}_{i\in I}$ is the minimal non-negative solution to the system of linear equations

$$\{\begin{array}{l}{h}_i^A=1\text{ for }i\in A\\ h_i^A={\sum }_j{p}_{ij}{h}_j^A\text{ for }i\notin A\end{array}$$

In matrix form $h^A=\tilde{P}{h}^A$ where $\tilde{P}$ is the matrix obtained by removing
the $i$-th row and column when $i\in A$.

Proof We first show that $h^A$ satisfies this equations. If $X_0=i\in A$ then $H^A=0$, so $h_i^A=1$ (is finite a.s.). If $i\notin A$

$$h_i^A={\mathbb{P}}_i(H^A<\infty )=\sum _{j\in I}{\mathbb{P}}_i(H^A<\infty \cap X_1=j)$$

since the events $X_1=j$ form a partition of $\Omega$. Using the definition of conditional probability

$$=\sum _{j\in I}{\mathbb{P}}_i(H^A<\infty |x_1=j){\mathbb{P}}_i(X_1=j)$$

note that ${\mathbb{P}}_i(X_1=k)=p_{ij}$. Given that $i\notin A$, $H^A\ge 1$. Then

$$H^A=\inf \{n\ge 0:X_n\in A\}=\inf \{n\ge 1:X_n\in A\}$$

We can define a “new” Markov chain ${\tilde{X}}_n:=X_{n+1}$ that w.r.t ${\mathbb{P}}_i(\cdot |X_1=j)$ is $Markov({\delta }_j,P)$ by the Markov property.

$${\mathbb{P}}_i(H^A<\infty |X_1=j)={\mathbb{P}}_j(H^A<\infty )=h_j^A$$

so that

$$h_i^A=\sum _{j\in I}{p}_{ij}{h}_j^A$$

Suppose now that $x=(x_i{)}_{i\in I}$ is any solution, then $h_i^A=x_i=1$ for $i\in A$. Suppose $i\notin A$, then

$$x_i=\sum _{j\in I}{p}_{ij}{x}_j=\sum _{j\in A}{p}_{ij}+\sum _{j\notin A}{p}_{ij}{x}_j$$

substitute for $x_j$ to obtain

$$x_i=\sum _{j\in A}{p}_{ij}+\sum _{j\notin A}{p}_{ij}\left(\sum _{k\in A}{p}_{jk}+\sum _{k\notin A}{p}_{jk}{x}_k\right)$$ $$={\mathbb{P}}_i(X_1\in A)+{\mathbb{P}}_i(X_1\notin A,X_2\in A)+\sum _{j\notin A}\sum _{k\notin A}{p}_{ij}{p}_{jk}{x}_k$$

we can reiterate the substitution, after $n$ steps one gets

$$={\mathbb{P}}_i(X_1\in A)+{\mathbb{P}}_i(X_1\notin A,X_2\in A)+\cdots +\sum _{J_1\notin A}\cdots \sum _{j_n\notin A}p\dots x_{j_n}$$

since $x$ is non-negative, so is the last term. Notice that the remaining terms add to the probability of ${\mathbb{P}}_i(H^A\le n)$ (each term is the probability of $H^A=l$. Then

$$x_i\ge {\mathbb{P}}_i(H^A\le n)$$

we can take the limit as $n\to \infty$ on both sides, and by Continuity of mesure we get the desired inequality. $\square$

Theorem The vector of mean hitting time $k^A=(k_i^A{)}_{i\in I}$ is the minimal non-negative solution to the system of linear equations

$$\{\begin{array}{l}{k}_i^A=0\text{ for }i\in A\\ k_i^A=1+{\sum }_j{p}_{ij}{k}_j^A\text{ for }i\notin A\end{array}$$

Proof First we show that $k^A$ solves these equations. $If$i \in A$then$k_i^A = 0$.If$i \notin A$ then, using first step analysis:

$$k_i^A=\sum _{n\ge 0}n{P}_i({\tau }_A=n)+\infty P_i({\tau }_A=\infty )=$$ $$\sum _{n\ge 0}\sum _{j\in I}n{P}_i({\tau }_A=n|X_1=j)P_i(X_1=j)+\sum _{j\in I}\infty P_i({\tau }_A=\infty |X_1=j)$$

we can exchange the sums by Fubini’s theorem (all the terms are non-negative), and $n\ge 1$ since $i\notin A$, and using the weak Markov property

$$=\sum _{j\in I}{p}_{ij}\left(\sum _{n\ge 1}n{P}_j({\tau }_A=n-1)+\infty P_j({\tau }_A=\infty )\right)$$

we now change the index to $m=n-1$

$$=\sum _{j\in I}{p}_{ij}\left(\sum _{m\ge 0}(m+1)P_j({\tau }_A=n)+\infty P_j({\tau }_A=\infty )\right)$$ $$=\sum _{j\in I}(p_{ij}{k}_j^A+1)\square$$

We need to prove that if $x_i$ is another non negative solution, then $k_i\le x_i$. The strategy is the same as in the previous proof (repeated substitution). Note that since $x_i=0$ if $i\in A$, we can omit these terms in the sum over all states. Let $i\notin A$, then

$$x_i=1+\sum _{j\notin A}{p}_{ij}{x}_j$$ $$=1+\sum _{j\notin A}{p}_{ij}\left(1+\sum _{k\notin I}{p}_{jk}{x}_k\right)$$ $$=1+\sum _{j\notin A}{p}_{ij}+\sum _{j\notin A}\sum _{k\notin A}{p}_{ij}{p}_{jk}{x}_k$$ $$=P_i({\tau }_A\ge 1)+P_i({\tau }_A\ge 2)+R$$

where $R\ge 0$, since $x$ is non-negative. Repeating the substitution $M$ times one gets:

$$x_i\ge \sum _{n=1}^M{P}_i({\tau }_A\ge n)$$

taking the limit $M\to \infty$ on both sides one gets the definition of $k_i^A$ on the right. $\square$